题目内容
已知函数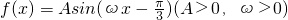 在某一个周期内的图象的最高点和最低点的坐标分别为(
在某一个周期内的图象的最高点和最低点的坐标分别为( ,2)(
,2)( ,-2).
,-2).
(1)求A和ω的值;
(2)已知α∈(0, ),且
),且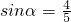 ,求f(α)的值.
,求f(α)的值.
解:(1)∵某一个周期内的图象的最高点和最低点的坐标分别为( ,2)(
,2)( ,-2).
,-2).
∴A=2,T=2×( -
- )=π
)=π
∴ω= =2
=2
∴A=2,ω=2
(2)∵α∈(0, ),且
),且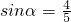 ,∴cosα=
,∴cosα=
∴sin2α= ,cos2α=1-2sin2α=-
,cos2α=1-2sin2α=-
由(1)知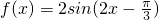
∴
=sin2α- cos2α
cos2α
= +
+
=
分析:(1)由函数图象最高点和最低点纵坐标可得振幅A值,相邻最高和最低点间的横坐标之差为半个周期,即可求得函数的周期,进而得ω的值
(2)先利用同角三角函数基本关系式和二倍角公式计算sin2α、cos2α的值,再利用(1)中结论,将f(α)化简,代入sin2α、cos2α的值求值即可
点评:本题主要考察了y=Asin(ωx+φ)型函数的图象和性质,三角变换公式在三角化简和求值中的应用,属基础题
 ,2)(
,2)( ,-2).
,-2).∴A=2,T=2×(
 -
- )=π
)=π∴ω=
 =2
=2∴A=2,ω=2
(2)∵α∈(0,
 ),且
),且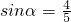 ,∴cosα=
,∴cosα=
∴sin2α=
 ,cos2α=1-2sin2α=-
,cos2α=1-2sin2α=-
由(1)知
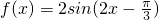
∴

=sin2α-
 cos2α
cos2α=
 +
+
=

分析:(1)由函数图象最高点和最低点纵坐标可得振幅A值,相邻最高和最低点间的横坐标之差为半个周期,即可求得函数的周期,进而得ω的值
(2)先利用同角三角函数基本关系式和二倍角公式计算sin2α、cos2α的值,再利用(1)中结论,将f(α)化简,代入sin2α、cos2α的值求值即可
点评:本题主要考察了y=Asin(ωx+φ)型函数的图象和性质,三角变换公式在三角化简和求值中的应用,属基础题

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
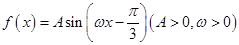 在某一个周期内的图象的最高点和最低点的坐标分别为
在某一个周期内的图象的最高点和最低点的坐标分别为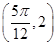 ,
,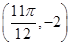 .
.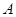 和
和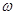 的值;
的值;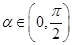 ,且
,且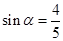 , 求
, 求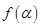 的值.
的值. 在某一个周期内的图象的最高点和最低点的坐标分别为(
在某一个周期内的图象的最高点和最低点的坐标分别为( ,2)(
,2)( ,-2).
,-2). ),且
),且 ,求f(α)的值.
,求f(α)的值.