题目内容
已知函数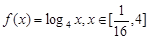 的值域为集合
的值域为集合 ,关于
,关于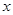 的不等式
的不等式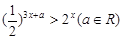 的解集为
的解集为 ,集合
,集合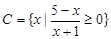 ,集合
,集合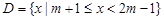
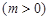
(1)若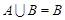 ,求实数
,求实数 的取值范围;
的取值范围;
(2)若 ,求实数
,求实数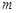 的取值范围。
的取值范围。
【答案】
(1) ;(2)
;(2) ,
,
【解析】
试题分析:(1)本小题主要考查不等式的解法、以及集合的基本关系,根据函数 单调性可求集合
单调性可求集合 ;利用
;利用 可求集合
可求集合 ;然后利用
;然后利用 可分析实数
可分析实数 的取值范围;(2)先解集合
的取值范围;(2)先解集合 ,然后根据
,然后根据 可分析实数
可分析实数 的取值范围
的取值范围
试题解析:(1)因为 ,所以
,所以 在
在 上,单调递增,
上,单调递增,
所以

 ,
2分
,
2分
又由 可得:
可得: 即:
即: ,所以
,所以 ,
,
所以 ,
4分
,
4分
又 所以可得:
所以可得: ,
5分
,
5分
所以 ,所以
,所以 即实数
即实数 的取值范围为
的取值范围为 6分
6分
(2)因为 ,所以有
,所以有 ,,所以
,,所以 ,
8分
,
8分
对于集合 有:
有:
①当 时,即
时,即 时
时 ,满足
,满足 10分
10分
②当 时,即
时,即 时
时 ,所以有:
,所以有:

 ,又因为
,又因为 ,所以
,所以 13分
13分
综上:由①②可得:实数 的取值范围为
的取值范围为 14分
14分
考点:不等式的解法,集合的基本关系

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目


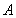

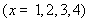
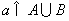
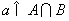
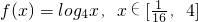 的值域为集合A,关于x的不等式
的值域为集合A,关于x的不等式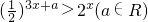 的解集为B,集合
的解集为B,集合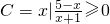 ,集合D={x|m+1≤x<2m-1}(m>0)
,集合D={x|m+1≤x<2m-1}(m>0)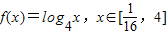 的值域为集合A,关于x的不等式
的值域为集合A,关于x的不等式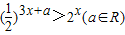 的解集为B,集合
的解集为B,集合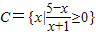 ,集合D={x|m+1≤x<2m-1}(m>0)
,集合D={x|m+1≤x<2m-1}(m>0)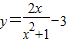 的值域为集合A,函数
的值域为集合A,函数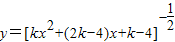 的定义域为集合B,若A∪B=B,求实数k的取值范围.
的定义域为集合B,若A∪B=B,求实数k的取值范围.