题目内容
已知函数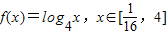 的值域为集合A,关于x的不等式
的值域为集合A,关于x的不等式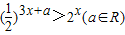 的解集为B,集合
的解集为B,集合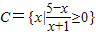 ,集合D={x|m+1≤x<2m-1}(m>0)
,集合D={x|m+1≤x<2m-1}(m>0)(1)若A∪B=B,求实数a的取值范围;
(2)若D⊆C,求实数m的取值范围.
【答案】分析:(1)利用对数函数的单调性求对数函数的值域A,解指数不等式求出B,再根据A⊆B可得-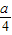 >1,由此求得实数a的取值范围.
>1,由此求得实数a的取值范围.
(2)解分式不等式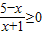 求得C,对于集合D={x|m+1≤x<2m-1}(m>0),由D⊆C,分D=∅和 D≠∅两种情况,分别求出实m的取值范围,再取并集,即得所求.
求得C,对于集合D={x|m+1≤x<2m-1}(m>0),由D⊆C,分D=∅和 D≠∅两种情况,分别求出实m的取值范围,再取并集,即得所求.
解答:解:(1)因为f(x)在[ ,4]上,单调递增,
,4]上,单调递增,
∵f(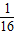 )=
)=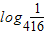 =-2,f(4)=log44=1,
=-2,f(4)=log44=1,
所以,A=[-2 1].--------------(2分)
又由关于x的不等式 可得 (2)-3x-a>2x,-3x-a>x x<-
可得 (2)-3x-a>2x,-3x-a>x x<-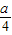 ,
,
所以,B=(-∞,-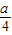 ).-----(4分)
).-----(4分)
又A∪B=B,∴A⊆B.--------(5分)
所以,-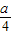 >1,a<-4,即实数a的取值范围为(-∞,-4).-------(6分)
>1,a<-4,即实数a的取值范围为(-∞,-4).-------(6分)
(2)因为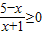 ,所以有
,所以有 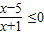 ,所以-1<x≤5,所以,C=(-1,5],---------(8分)
,所以-1<x≤5,所以,C=(-1,5],---------(8分)
对于集合D={x|m+1≤x<2m-1}(m>0),若D⊆C,有:
①当 m+1≥2m-1时,即 0<m≤2时,D=∅,满足 D⊆C.-----------(10分)
②当 m+1<2m-1 时,即 m>2时,D≠∅,所以有: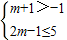 ,解得-2<m≤3,又 m>2,2<m≤3.---------(13分)
,解得-2<m≤3,又 m>2,2<m≤3.---------(13分)
综上:由①②可得:实m的取值范围为(0,3].---------(14分)
点评:本题主要考查利用对数函数的单调性求值域,指数不等式、分式不等式的解法,集合间的包含关系,属于中档题.
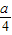 >1,由此求得实数a的取值范围.
>1,由此求得实数a的取值范围.(2)解分式不等式
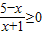 求得C,对于集合D={x|m+1≤x<2m-1}(m>0),由D⊆C,分D=∅和 D≠∅两种情况,分别求出实m的取值范围,再取并集,即得所求.
求得C,对于集合D={x|m+1≤x<2m-1}(m>0),由D⊆C,分D=∅和 D≠∅两种情况,分别求出实m的取值范围,再取并集,即得所求.解答:解:(1)因为f(x)在[
 ,4]上,单调递增,
,4]上,单调递增,∵f(
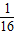 )=
)=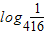 =-2,f(4)=log44=1,
=-2,f(4)=log44=1,所以,A=[-2 1].--------------(2分)
又由关于x的不等式
 可得 (2)-3x-a>2x,-3x-a>x x<-
可得 (2)-3x-a>2x,-3x-a>x x<-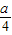 ,
,所以,B=(-∞,-
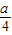 ).-----(4分)
).-----(4分)又A∪B=B,∴A⊆B.--------(5分)
所以,-
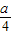 >1,a<-4,即实数a的取值范围为(-∞,-4).-------(6分)
>1,a<-4,即实数a的取值范围为(-∞,-4).-------(6分)(2)因为
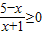 ,所以有
,所以有 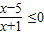 ,所以-1<x≤5,所以,C=(-1,5],---------(8分)
,所以-1<x≤5,所以,C=(-1,5],---------(8分)对于集合D={x|m+1≤x<2m-1}(m>0),若D⊆C,有:
①当 m+1≥2m-1时,即 0<m≤2时,D=∅,满足 D⊆C.-----------(10分)
②当 m+1<2m-1 时,即 m>2时,D≠∅,所以有:
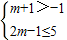 ,解得-2<m≤3,又 m>2,2<m≤3.---------(13分)
,解得-2<m≤3,又 m>2,2<m≤3.---------(13分)综上:由①②可得:实m的取值范围为(0,3].---------(14分)
点评:本题主要考查利用对数函数的单调性求值域,指数不等式、分式不等式的解法,集合间的包含关系,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


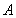

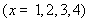
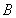
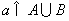
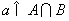
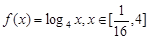 的值域为集合
的值域为集合 ,关于
,关于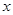 的不等式
的不等式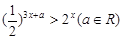 的解集为
的解集为 ,集合
,集合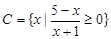 ,集合
,集合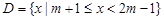
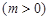
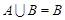 ,求实数
,求实数 的取值范围;
的取值范围; ,求实数
,求实数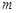 的取值范围。
的取值范围。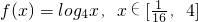 的值域为集合A,关于x的不等式
的值域为集合A,关于x的不等式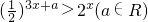 的解集为B,集合
的解集为B,集合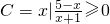 ,集合D={x|m+1≤x<2m-1}(m>0)
,集合D={x|m+1≤x<2m-1}(m>0)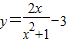 的值域为集合A,函数
的值域为集合A,函数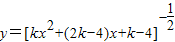 的定义域为集合B,若A∪B=B,求实数k的取值范围.
的定义域为集合B,若A∪B=B,求实数k的取值范围.