题目内容
已知函数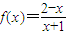 ;
;(1)求出函数f(x)的对称中心;
(2)证明:函数f(x)在(-1,+∞)上为减函数;
(3)是否存在负数x,使得
 成立,若存在求出x;若不存在,请说明理由.
成立,若存在求出x;若不存在,请说明理由.
【答案】分析:(1)先对函数利用分离常数的方法进行化简变形,再根据解析式与反比例函数进行比较,求出对称中心;
(2)直接利用单调减函数的定义进行证明,先在(-1,+∞)上任取两点,并规定大小关系,将它们的函数值进行作差,判定符号即可;
(3)假设存在负数x分别计算出函数f(x)的值域与函数3x的值域,找两个值域之间是否存在交集,从而找出矛盾即可.
解答:解:(1)∵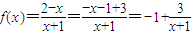
∴函数f(x)的对称中心为(-1,-1)
(2)任取x1,x2∈(-1,+∞),且x1<x2
∵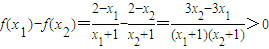
∴函数f(x)在(-1,+∞)上为减函数
(3)不存在
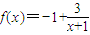 ,
,
由x<0得:f(x)<-1或f(x)>2但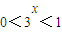 ,
,
所以不存在.
点评:本题主要考查了函数单调性的证明与判定,以及函数恒成立问题与对称中心的求解,属于中档题.
(2)直接利用单调减函数的定义进行证明,先在(-1,+∞)上任取两点,并规定大小关系,将它们的函数值进行作差,判定符号即可;
(3)假设存在负数x分别计算出函数f(x)的值域与函数3x的值域,找两个值域之间是否存在交集,从而找出矛盾即可.
解答:解:(1)∵
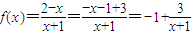
∴函数f(x)的对称中心为(-1,-1)
(2)任取x1,x2∈(-1,+∞),且x1<x2
∵
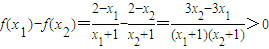
∴函数f(x)在(-1,+∞)上为减函数
(3)不存在
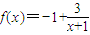 ,
,由x<0得:f(x)<-1或f(x)>2但
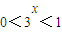 ,
,所以不存在.
点评:本题主要考查了函数单调性的证明与判定,以及函数恒成立问题与对称中心的求解,属于中档题.

练习册系列答案
相关题目
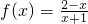 ;
;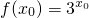 成立,若存在求出x0;若不存在,请说明理由.
成立,若存在求出x0;若不存在,请说明理由.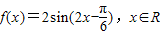 ,
,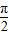 ]上的最小值和最大值,并求出取得最值时x的值.
]上的最小值和最大值,并求出取得最值时x的值. .
. 时,证明函数y=f(x)图象在点
时,证明函数y=f(x)图象在点 处切线的下方;
处切线的下方; ,且a+b+c=1,证明:
,且a+b+c=1,证明: ”;
”; 的最大值.(只指出正确结论,不要求证明)
的最大值.(只指出正确结论,不要求证明)