题目内容
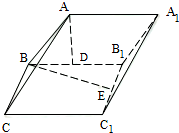
7.在直四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,AB=2,BC=1,AA1=$\sqrt{2}$,E,F分别是C1D1,A1B的中点.(1)证明:EF⊥A1C;
(2)求三棱锥A1-BCE的体积.
分析 (1)取B1B的中点M,连接C1M,B1C,FM,证明:C1M⊥平面A1B1C,可得结论;
(2)连接D1C,作C1N⊥D1C,则C1N为C1到平面A1C的距离,由等面积可得C1N,利用转化底面的方法,求出三棱锥A1-BCE的体积.
解答  (1)证明:取B1B的中点M,连接C1M,B1C,FM,则
(1)证明:取B1B的中点M,连接C1M,B1C,FM,则
四边形EFMC1是平行四边形,所以EF∥C1M.
由题意,AB=2,BC=1,AA1=$\sqrt{2}$,可得△C1B1M∽△B1C1C,
∴C1M⊥B1C,
∵A1B1⊥平面B1C,
∴A1B1⊥C1M,
∵A1B1∩B1C=B1,
∴C1M⊥平面A1B1C,
∵A1C?平面A1B1C,
∴C1M⊥A1C,
∴EF⊥A1C;
(2)解:由题意,A1B=$\sqrt{6}$,∴${S}_{△{A}_{1}BC}=\frac{1}{2}×\sqrt{6}×1$=$\frac{\sqrt{6}}{2}$
连接D1C,作C1N⊥D1C,则C1N为C1到平面A1C的距离,由等面积可得C1N=$\frac{2×\sqrt{2}}{\sqrt{6}}$=$\frac{2}{\sqrt{3}}$,
∴E到平面A1C的距离为$\frac{1}{\sqrt{3}}$,
∴三棱锥A1-BCE的体积=$\frac{1}{3}×\frac{\sqrt{6}}{2}×\frac{1}{\sqrt{3}}$=$\frac{\sqrt{2}}{6}$.
点评 本题考查线面垂直的判定与性质,考查三棱锥体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 如图,在直三棱柱ABC-A1B1C1中,D、E分别是棱A1B1、CC1的点,且DC1⊥A1B1,A1D=$\frac{2}{3}$A1B1,CE=$\frac{1}{3}$CC1,求证:
如图,在直三棱柱ABC-A1B1C1中,D、E分别是棱A1B1、CC1的点,且DC1⊥A1B1,A1D=$\frac{2}{3}$A1B1,CE=$\frac{1}{3}$CC1,求证: 如图,ABCD是正方形,DE⊥平面ABCD,AF∥DE,DE=DA=3AF.
如图,ABCD是正方形,DE⊥平面ABCD,AF∥DE,DE=DA=3AF. 已知四棱锥P-ABCD中,底面ABCD是菱形,M是PC的中点,∠PDC=90°,∠PDA=90°,∠DAB=60°
已知四棱锥P-ABCD中,底面ABCD是菱形,M是PC的中点,∠PDC=90°,∠PDA=90°,∠DAB=60°