题目内容
若非零函数 对任意实数
对任意实数 均有
均有 ,且当
,且当 时
时
(1)求证: ;
;
(2)求证: 为R上的减函数;
为R上的减函数;
(3)当 时, 对
时, 对 时恒有
时恒有 ,求实数
,求实数 的取值范围.
的取值范围.
 对任意实数
对任意实数 均有
均有 ,且当
,且当 时
时
(1)求证:
 ;
;(2)求证:
 为R上的减函数;
为R上的减函数;(3)当
 时, 对
时, 对 时恒有
时恒有 ,求实数
,求实数 的取值范围.
的取值范围.(1)证法一: 即
即 又
又

当 时,
时,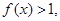
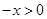
 则
则
故对于 恒有
恒有
证法二: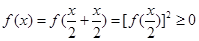
 为非零函数
为非零函数 
(2)证明:令 且
且
有 , 又
, 又 即
即
故 又
又

故 为R上的减函数
为R上的减函数
(3)实数 的取值范围为
的取值范围为
 即
即 又
又

当
 时,
时,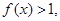
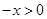
 则
则
故对于
 恒有
恒有
证法二:
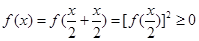
 为非零函数
为非零函数 
(2)证明:令
 且
且
有
 , 又
, 又 即
即
故
 又
又

故
 为R上的减函数
为R上的减函数(3)实数
 的取值范围为
的取值范围为
试题分析:(1)由题意可取
 代入等式
代入等式 ,得出关于
,得出关于 的方程,因为
的方程,因为 为非零函数,故
为非零函数,故 ,再令
,再令 代入等式,可证
代入等式,可证 ,从而证明当
,从而证明当 时,有
时,有 ;(2)着眼于减函数的定义,利用条件当
;(2)着眼于减函数的定义,利用条件当 时,有
时,有 ,根据等式
,根据等式 ,令
,令 ,
, ,可得
,可得 ,从而可证该函数为减函数.(3)根据
,从而可证该函数为减函数.(3)根据 ,由条件
,由条件 可求得
可求得 ,将
,将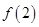 替换不等式中的
替换不等式中的 ,再根据函数的单调性可得
,再根据函数的单调性可得 ,结合
,结合 的范围,从而得解.
的范围,从而得解.试题解析:(1)证法一:
 即
即 又
又
当
 时,
时,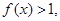
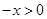
 则
则
故对于
 恒有
恒有 4分
4分证法二:
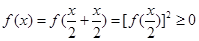
 为非零函数
为非零函数 
(2)令
 且
且
有
 , 又
, 又 即
即
故
 又
又

故
 为R上的减函数 8分
为R上的减函数 8分(3)
 故
故 , 10分
, 10分则原不等式可变形为

依题意有
 对
对 恒成立
恒成立 或
或 或
或
故实数
 的取值范围为
的取值范围为 13分
13分
练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 ,如果每年平均增长5﹪,经过
,如果每年平均增长5﹪,经过 年,树林中有木材
年,树林中有木材
 ,
, )
) 的正方形
的正方形 ,点
,点 分别在边
分别在边 和
和 上,△
上,△ ,△
,△ 和四边形
和四边形 均由单一材料制成,制成△
均由单一材料制成,制成△ 的三种材料的每平方米价格之比依次为3:2:1.若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分构成四边形
的三种材料的每平方米价格之比依次为3:2:1.若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分构成四边形 .则当
.则当

 关于时间
关于时间 的函数关系式分别为
的函数关系式分别为 ,
, ,
, ,
, ,有以下结论:
,有以下结论: 时,甲走在最前面;
时,甲走在最前面; 时,丁走在最前面,当
时,丁走在最前面,当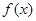 满足
满足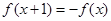 ,且
,且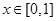 时,
时,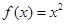 ,若在区间
,若在区间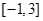 内,函数
内,函数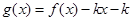 有4个零点,则实数
有4个零点,则实数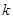 的取值范围是( )
的取值范围是( )
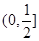


 有三个不同的实数根,则实数
有三个不同的实数根,则实数 的取值范围是( )
的取值范围是( )



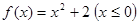 的反函数
的反函数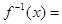 _____________.
_____________. ,则等式
,则等式 的解集是( )
的解集是( )

 或
或
 或
或