题目内容
设命题p：函数y=cos2x的最小正周期为
；命题q：函数f（x）=sin（x-
）的图象的一条对称轴是x=-
，则下列判断正确的是（ ）
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
分析：命题p：由函数y=cosωx的最小正周期为
知命题p为假命题；命题q：由于函数f（x）=sin（x-
）在x=-
时的函数值是-1，则命题q为真命题．再结合复合命题的真假判断，对四个选项一一检验，即可得到正确答案．
| 2π |
| ω |
| π |
| 4 |
| π |
| 4 |
解答：解：由于函数y=cosωx的最小正周期为
知，
命题p：函数y=cos2x的最小正周期为
，为假命题；
由于函数f（x）=sin（x-
）在x=-
时的函数值是-1，
则命题q：函数f（x）=sin（x-
）的图象的一条对称轴是x=-
，为真命题．
故p∧q为假，p∨q为真，￢q为假，
故答案选 B．
| 2π |
| ω |
命题p：函数y=cos2x的最小正周期为
| π |
| 2 |
由于函数f（x）=sin（x-
| π |
| 4 |
| π |
| 4 |
则命题q：函数f（x）=sin（x-
| π |
| 4 |
| π |
| 4 |
故p∧q为假，p∨q为真，￢q为假，
故答案选 B．
点评：本题考查的知识点是复合命题的真假判定，解决的办法是根据三角函数的性质先判断组成复合命题的简单命题的真假，再根据真值表进行判断．
练习册系列答案
相关题目
，3]时，函数f（x）=x+
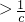恒成立．如果p或q为真命题，p且q为假命题，求c的取值范围．
，3]时，函数f（x）=x+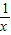
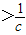恒成立．如果p或q为真命题，p且q为假命题，求c的取值范围．