题目内容
设函数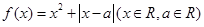 .
.
(1)讨论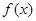 的奇偶性;
的奇偶性;
(2)当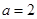 时,求
时,求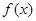 的单调区间;
的单调区间;
(3)若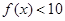 对
对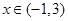 恒成立,求实数
恒成立,求实数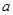 的取值范围.
的取值范围.
【答案】
(1)当a=0是偶函数;当a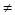 0时函数f(x)为非奇非偶函数
0时函数f(x)为非奇非偶函数
(2) 原函数的减区间为(-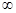 ,
,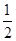 ),增区间为(
),增区间为(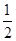 ,+
,+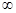 );(3)
);(3) 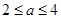
【解析】
试题分析:解:(1)i)当a=0时:f(x)=x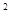 +
+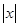
∵f(-x)="(-x)+"  =x
=x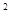 +
+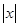 =f(x)
=f(x)
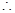 函数f(x)为偶函数3分
函数f(x)为偶函数3分
ii)当a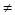 0时:
0时:
∵f(1)=1+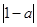 ,f(-1)=1+
,f(-1)=1+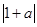
若f(1)=f(-1),则1+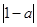 =1+
=1+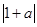 从而a=0,舍去;
从而a=0,舍去;
若f(1)=-f(-1),则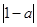 +
+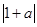 =-2从而a
=-2从而a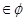
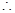 f(1)
f(1)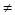 ±f(-1),
±f(-1), 函数f(x)为非奇非偶函数6分
函数f(x)为非奇非偶函数6分
(2)当a=2时:
f(x)=x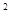 +
+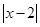 =
=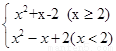
 原函数的减区间为(-
原函数的减区间为(-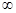 ,
,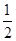 ),增区间为(
),增区间为(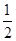 ,+
,+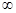 );10分
);10分
(3)∵x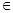 (-1,3)
(-1,3)
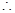 f(x)<10可变为x
f(x)<10可变为x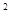 -10<a-x< 10-x
-10<a-x< 10-x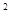
即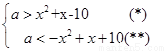
对(*):令g(x)= x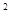 +x-10,其对称轴为
+x-10,其对称轴为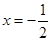
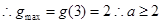 ③
③
对②令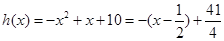
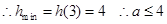 ④
④
由③、④知: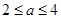 16分
16分
考点:函数性质的综合运用
点评:主要是考查了函数奇偶性和单调性以及函数的最值的运用,属于基础题。

练习册系列答案
相关题目
 ,
,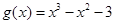 .
.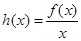 的单调性;
的单调性;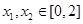 ,使得
,使得 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数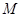 ;
; ,都有
,都有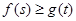 成立,求实数
成立,求实数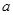 的取值范围.
的取值范围.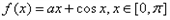 。
。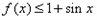 ,求a的取值范围。
,求a的取值范围。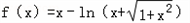 .
.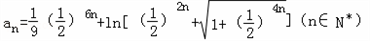 ,试证明:
,试证明: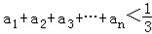 .
.