题目内容
设函数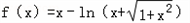 .
.
(1) 讨论函数f(x)的单调性;
(2)若x≥0时,恒有f(x)≤ax3,试求实数a的取值范围;
(3)令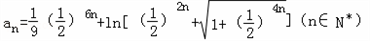 ,试证明:
,试证明: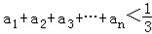 .
.
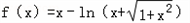 .
.(1) 讨论函数f(x)的单调性;
(2)若x≥0时,恒有f(x)≤ax3,试求实数a的取值范围;
(3)令
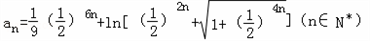 ,试证明:
,试证明: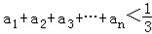 .
.解:(I)函数的定义域为R, 由于f'(x)=1﹣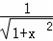 ≥0,知
≥0,知
f(x)是R上的增函数.
(II)令g(x)=g(x)﹣ax3=x﹣ln(x+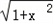 )﹣ax3.则
)﹣ax3.则
g'(x)=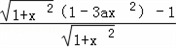 ,
,
令h(x)=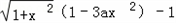 ,则
,则
h'(x)=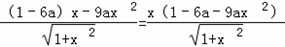 ,
,
(1)当a≥ 时,h'(x)≤0,从而h(x)是[0,+∞)上的减函数,
时,h'(x)≤0,从而h(x)是[0,+∞)上的减函数,
因h(0)=0,则x≥0时,h(x)≤0,也即g'(x)≤0,
进而g(x)是[0,+∞)上的减函数,
注意g(0)=0,则x≥0时,g(x)≤0,也即f(x)≤ax3,
(2)当0<a< 时,在[0,
时,在[0,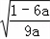 ],h'(x)>0,
],h'(x)>0,
从而x∈[0,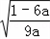 ]时,也即f(x)>ax3,
]时,也即f(x)>ax3,
(3)当a≤0时,h'(x)>0,同理可知:f(x)>ax3,
综合,实数a的取值范围[ ,+∞).
,+∞).
(III)在(II)中取a= ,则
,则
x∈[0,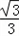 ],时,x﹣ln(x+
],时,x﹣ln(x+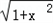 )>
)> x3,即
x3,即  x3+ln(x+
x3+ln(x+ )<x,
)<x,
令x=( )2n,则
)2n,则
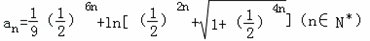 <(
<( )2n,
)2n,
∴
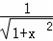 ≥0,知
≥0,知f(x)是R上的增函数.
(II)令g(x)=g(x)﹣ax3=x﹣ln(x+
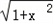 )﹣ax3.则
)﹣ax3.则g'(x)=
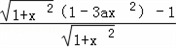 ,
,令h(x)=
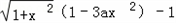 ,则
,则h'(x)=
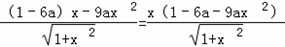 ,
,(1)当a≥
 时,h'(x)≤0,从而h(x)是[0,+∞)上的减函数,
时,h'(x)≤0,从而h(x)是[0,+∞)上的减函数,因h(0)=0,则x≥0时,h(x)≤0,也即g'(x)≤0,
进而g(x)是[0,+∞)上的减函数,
注意g(0)=0,则x≥0时,g(x)≤0,也即f(x)≤ax3,
(2)当0<a<
 时,在[0,
时,在[0, ],h'(x)>0,
],h'(x)>0,从而x∈[0,
 ]时,也即f(x)>ax3,
]时,也即f(x)>ax3,(3)当a≤0时,h'(x)>0,同理可知:f(x)>ax3,
综合,实数a的取值范围[
 ,+∞).
,+∞).(III)在(II)中取a=
 ,则
,则x∈[0,
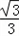 ],时,x﹣ln(x+
],时,x﹣ln(x+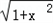 )>
)> x3,即
x3,即  x3+ln(x+
x3+ln(x+ )<x,
)<x,令x=(
 )2n,则
)2n,则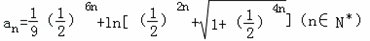 <(
<( )2n,
)2n,∴


练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 ,
,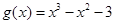 .
.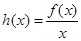 的单调性;
的单调性;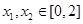 ,使得
,使得 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数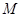 ;
; ,都有
,都有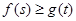 成立,求实数
成立,求实数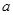 的取值范围.
的取值范围.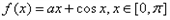 。
。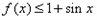 ,求a的取值范围。
,求a的取值范围。