题目内容
已知 ,
, 是任意两个向量,下列条件:①
是任意两个向量,下列条件:① =
= ;②|
;②| |=|
|=| |;③
|;③ 与
与 的方向相反;④
的方向相反;④ =
= 或
或 =
= ;⑤
;⑤ 与
与 都是单位向量,其中为向量
都是单位向量,其中为向量 与
与 共线的充分不必要条件的个数是
共线的充分不必要条件的个数是
- A.1
- B.2
- C.3
- D.4
C
分析:若两向量:① =
= ;③
;③ 与
与 的方向相反;④
的方向相反;④ =
= 或
或 =
= ;则两向量互为相反,一定共线,而当两向量共线时,不一定是:①
;则两向量互为相反,一定共线,而当两向量共线时,不一定是:① =
= ;③
;③ 与
与 的方向相反;④
的方向相反;④ =
= 或
或 =
= ;由此关系判断即可.
;由此关系判断即可.
解答:若“:① =
= ;则“
;则“ ”与“
”与“ ”共线,但反之不一定成立,
”共线,但反之不一定成立,
若③ 与
与 的方向相反;则“
的方向相反;则“ ”与“
”与“ ”一定共线,但反之不一定成立,
”一定共线,但反之不一定成立,
若④ =
= 或
或 =
= ;则“
;则“ ”与“
”与“ ”一定共线,但反之不一定成立,
”一定共线,但反之不一定成立,
由此知 ①③④为向量 与
与 共线的充分不必要条件;
共线的充分不必要条件;
故选C.
点评:本题考查平行向量与共线向量,解题的关键是熟练掌握理解共线向量的定义以及相反向量的定义,结合向量的数乘,进行判断;本题还考查的知识点是充要条件的定义,根据充要条件的定义,先判断p?q,再判断q?p的真假,再得到结论.
分析:若两向量:①
 =
= ;③
;③ 与
与 的方向相反;④
的方向相反;④ =
= 或
或 =
= ;则两向量互为相反,一定共线,而当两向量共线时,不一定是:①
;则两向量互为相反,一定共线,而当两向量共线时,不一定是:① =
= ;③
;③ 与
与 的方向相反;④
的方向相反;④ =
= 或
或 =
= ;由此关系判断即可.
;由此关系判断即可.解答:若“:①
 =
= ;则“
;则“ ”与“
”与“ ”共线,但反之不一定成立,
”共线,但反之不一定成立,若③
 与
与 的方向相反;则“
的方向相反;则“ ”与“
”与“ ”一定共线,但反之不一定成立,
”一定共线,但反之不一定成立,若④
 =
= 或
或 =
= ;则“
;则“ ”与“
”与“ ”一定共线,但反之不一定成立,
”一定共线,但反之不一定成立,由此知 ①③④为向量
 与
与 共线的充分不必要条件;
共线的充分不必要条件;故选C.
点评:本题考查平行向量与共线向量,解题的关键是熟练掌握理解共线向量的定义以及相反向量的定义,结合向量的数乘,进行判断;本题还考查的知识点是充要条件的定义,根据充要条件的定义,先判断p?q,再判断q?p的真假,再得到结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
,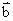 是任意两个向量,下列条件:(1)
是任意两个向量,下列条件:(1)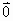 或
或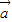 ,
,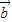 是任意两个向量,下列条件:①
是任意两个向量,下列条件:①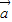 =
=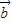 ;②|
;②| |=|
|=| |;③
|;③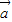 与
与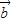 的方向相反;④
的方向相反;④ =
= 或
或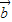 =
=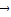 ;⑤
;⑤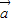 与
与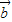 都是单位向量,其中为向量
都是单位向量,其中为向量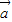 与
与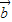 共线的充分不必要条件的个数是( )
共线的充分不必要条件的个数是( )