题目内容
已知向量a=(1,2cos2 wx-1),b=(sinwx,1)(w>0),函数f(x)=a•b(x∈R)最小正周期为2π.
wx-1),b=(sinwx,1)(w>0),函数f(x)=a•b(x∈R)最小正周期为2π.
(1) 求y=f(x)的解析式,并求函数的单调递增区间;
(2) 若f(a)= ,a∈(0,
,a∈(0, ),求sina的值.
),求sina的值.
解:(1)∵
∴
又函数的最小正周期T=2π
故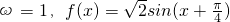
由 可得
可得 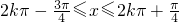
函数的单调递增区间为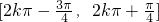
(2)因为
即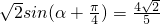
∴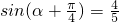
又
∴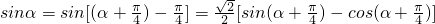 =
=
分析:(1)利用向量数量积的坐标表示及辅助角公式可得,f(x)= ,利用周期公式T=
,利用周期公式T= 可求ω=1,由
可求ω=1,由 可求单调增区间
可求单调增区间
(2))由 可求sin(
可求sin( ),cos(
),cos( ),而sin
),而sin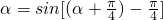 ,利用两角差的正弦公式展开可求
,利用两角差的正弦公式展开可求
点评:本题主要考查了向量的数量积的坐标表示,辅助角公式的应用,三角函数的周期公式,正弦函数的单调区间的求解,拆角的技巧在解题中的应用,是一道综合性较好的试题.

∴

又函数的最小正周期T=2π
故
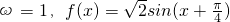
由
 可得
可得 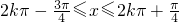
函数的单调递增区间为
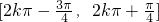
(2)因为

即
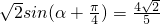
∴
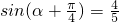
又

∴
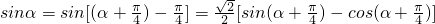 =
=
分析:(1)利用向量数量积的坐标表示及辅助角公式可得,f(x)=
 ,利用周期公式T=
,利用周期公式T= 可求ω=1,由
可求ω=1,由 可求单调增区间
可求单调增区间(2))由
 可求sin(
可求sin( ),cos(
),cos( ),而sin
),而sin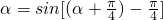 ,利用两角差的正弦公式展开可求
,利用两角差的正弦公式展开可求点评:本题主要考查了向量的数量积的坐标表示,辅助角公式的应用,三角函数的周期公式,正弦函数的单调区间的求解,拆角的技巧在解题中的应用,是一道综合性较好的试题.

练习册系列答案
相关题目