题目内容
探究函数 的最小值,并确定取得最小值时x的值,列表如下:
的最小值,并确定取得最小值时x的值,列表如下:
|
x |
… |
0.5 |
1 |
1.5 |
1.7 |
1.9 |
2 |
2.1 |
2.2 |
2.3 |
3 |
4 |
5 |
7 |
… |
|
y |
… |
8.5 |
5 |
4.17 |
4.05 |
4.005 |
4 |
4.005 |
4.002 |
4.04 |
4.3 |
5 |
5.8 |
7.57 |
… |
请观察表中y值随x值变化的特点,完成以下问题:
(1)函数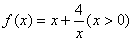 在区间 上递增.
在区间 上递增.
当 时,y最小 = .
(2)函数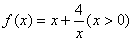 在区间 上递减,并用定义证明之;
在区间 上递减,并用定义证明之;
(3)函数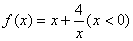 时,有最值吗?是最大值还是最小值?此时x为何值?
时,有最值吗?是最大值还是最小值?此时x为何值?
(写出结果,简要说明理由)
解:(1)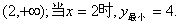 …………2分
…………2分
(2)(0,2)
证明:设x1,x2是区间(0,2)上的任意两个实数,且x1 < x2.
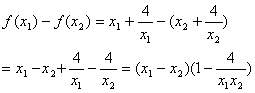
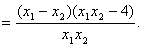 …………6分
…………6分
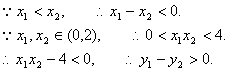
∴函数在(0,2)上单调递减. …………8分
(3)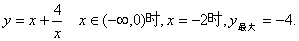 …………10分
…………10分
因为函数 是奇函数;
是奇函数;
当x > 0时,函数在x = 2时取得小最值4,不存在最大值;
因此当x < 0时,函数在x =-2时取得最大值-4,不存在最小值…………12分

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案探究函数![]() 的最小值,并确定取得最小值时x的值.列表如下:
的最小值,并确定取得最小值时x的值.列表如下:
x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 4.8 | 7.57 | … |
请观察表中y值随x值变化的特点,完成以下的问题.
函数![]() 在区间(0,2)上递减;
在区间(0,2)上递减;
函数![]() 在区间 上递增.
在区间 上递增.
当![]() 时,
时,![]() .
.
证明:函数![]() 在区间(0,2)递减.
在区间(0,2)递减.
思考:
函数探究函数![]() 的最小值,并确定取得最小值时x的值.列表如下:
的最小值,并确定取得最小值时x的值.列表如下:
x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
请观察表中y值随x值变化的特点,完成以下的问题.
(1)函数![]() 在区间(0,2)上递减,在区间 上递增. 当
在区间(0,2)上递减,在区间 上递增. 当![]() 时,
时,![]() .
.
(2)证明:函数![]() 在区间(0,2)递减.
在区间(0,2)递减.
(3)思考?函数![]() 时有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
时有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
 的最小值,并确定取得最小值时x的值.列表如下:
的最小值,并确定取得最小值时x的值.列表如下:| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
函数
 在区间(0,2)上递减;
在区间(0,2)上递减;(1)函数
 在区间______上递增.当x=______时,y最小=______.
在区间______上递增.当x=______时,y最小=______.(2)证明:函数
 在区间(0,2)递减.
在区间(0,2)递减.(3)思考:函数
 有最值吗?如有,是最大值还是最小值?此时x为何值?(直接回答结果,不需证明).
有最值吗?如有,是最大值还是最小值?此时x为何值?(直接回答结果,不需证明). 的最小值,并确定取得最小值时x的值.列表如下:
的最小值,并确定取得最小值时x的值.列表如下:| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.002 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
(1)函数
 在区间(0,2)上递减,函数
在区间(0,2)上递减,函数 在区间______上递增;
在区间______上递增;(2)函数
 ,当x=______时,y最小=______;
,当x=______时,y最小=______;(3)函数
 时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明) 的最小值,并确定取得最小值时x的值.列表如下,请观察表中y值随x值变化的特点,完成以下的问题.
的最小值,并确定取得最小值时x的值.列表如下,请观察表中y值随x值变化的特点,完成以下的问题.| x | … | 0.5 | 1 | 1.5 | 1.7 | 2 | 2.1 | 2.3 | 3 | 4 | 7 | … |
| y | … | 64.25 | 17 | 9.36 | 8.43 | 8 | 8.04 | 8.31 | 10.7 | 17 | 49.33 | … |
 在区间(0,2)上递减,问:
在区间(0,2)上递减,问:(1)函数
 在区间______上递增.当x=______时,y最小=______.
在区间______上递增.当x=______时,y最小=______.(2)证明:函数
 在区间(0,2)递减;
在区间(0,2)递减;(3)思考:函数
 有最大值或最小值吗?如有,是多少?此时x为何值?(直接回答结果,不需证明)
有最大值或最小值吗?如有,是多少?此时x为何值?(直接回答结果,不需证明)