题目内容
已知双曲线
-
=1的准线过椭圆
+
=1的焦点，则直线y=kx+2与椭圆至多有一个交点的充要条件是________．
k∈[-
，]
分析：先求得准线方程，可推知a和b的关系，进而根据c2=a2-b2求得b，椭圆的方程可得，与直线y=kx+2联立消去y，根据判别式小于等于0求得k的范围．
解答：根据题意，易得准线方程是x=±
=±1
所以c2=a2-b2=4-b2=1即b2=3
所以方程是
联立y=kx+2可得3x2+（4k2+16k）x+4=0
由△≤0解得K∈[-，]
故答案为：k∈[-，]．
点评：本题主要考查了直线与圆锥曲线的综合问题．解题的关键是先根据椭圆的性质求出椭圆的方程．
，]分析：先求得准线方程，可推知a和b的关系，进而根据c2=a2-b2求得b，椭圆的方程可得，与直线y=kx+2联立消去y，根据判别式小于等于0求得k的范围．
解答：根据题意，易得准线方程是x=±
=±1所以c2=a2-b2=4-b2=1即b2=3
所以方程是
联立y=kx+2可得3x2+（4k2+16k）x+4=0
由△≤0解得K∈[-
，]故答案为：k∈[-
，]．点评：本题主要考查了直线与圆锥曲线的综合问题．解题的关键是先根据椭圆的性质求出椭圆的方程．
练习册系列答案
优学名师名题系列答案
相关题目
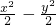=1的准线经过椭圆
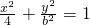（b＞0）的焦点，则b=________．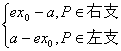
-
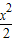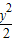=1的准线方程为x=±
,且P(x0,y0)是双曲线上任一点,F是其右焦点,则|PF|=
-
=1的准线过椭圆
+
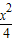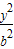=1的焦点，则直线y=kx+2与椭圆至多有一个交点的充要条件是 ．
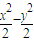=1的准线经过椭圆
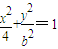（b＞0）的焦点，则b= ．