题目内容
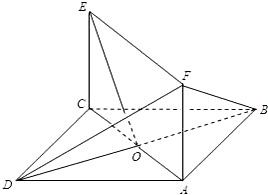 如图所示,正方形ABCD和矩形ACEF所在的平面相互垂直,已知AB=2,AF=
如图所示,正方形ABCD和矩形ACEF所在的平面相互垂直,已知AB=2,AF=| 2 |
(I)求证:EO⊥平面BDF;
(II)求二面角A-DF-B的大小.
分析:(I)求证EO⊥平面BDF,由面面垂直关系及正方形的性质易得EO⊥BD,再由题设中的条件易得∠EOF=90°;
(II)求二面角A-DF-B的大小需先做角,可过O作OP⊥AD于P,过P作PM⊥DF于M,连接OM,可证得∠OMP即二面角的平面角,由于这个三角形是直角三角形,平面角易求.
(II)求二面角A-DF-B的大小需先做角,可过O作OP⊥AD于P,过P作PM⊥DF于M,连接OM,可证得∠OMP即二面角的平面角,由于这个三角形是直角三角形,平面角易求.
解答:证明:(I)如图,正方形ABCD和矩形ACEF所在的平面相互垂直,对角线BD⊥AC,故有BD⊥平面ACEF,又EO?平面ACEF,故得BD⊥EO
又AB=2,AF=
.可求得AC=2
,即CO=AO=AF=CE=
,由于三角形ECO与三角形FAO都是直角三角形,故可得∠EOC=∠FOA=45°,所以∠EOF=90°,即EO⊥OF
又FO∩BD=O,故有EO⊥平面BDF
(II)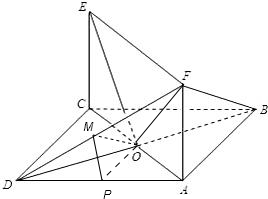 过O作OP⊥AD于P,过P作PM⊥DF于M,连接OM,
过O作OP⊥AD于P,过P作PM⊥DF于M,连接OM,
由题设条件知F-AD-O是直二面角,故可得OP⊥面ADF,由此可得OP⊥DF,由作图,PM⊥DF,故有DF⊥面OMP,所以OM⊥DF,由此可证得∠OMP即二面角的平面角,
在直线三角形DOA中,由于OA=OD,故P是AD中点,易得OP=1
在直角三角形DAF中可求得DF=
,由P是中点得DP=1,
由于△DAF≈△DMP,故有
=
得MP=
=
=
在直角三角形OPM中,tan∠OMP=
=
=
二面角A-DF-B的大小为60°
又AB=2,AF=
| 2 |
| 2 |
| 2 |
又FO∩BD=O,故有EO⊥平面BDF
(II)
 过O作OP⊥AD于P,过P作PM⊥DF于M,连接OM,
过O作OP⊥AD于P,过P作PM⊥DF于M,连接OM,由题设条件知F-AD-O是直二面角,故可得OP⊥面ADF,由此可得OP⊥DF,由作图,PM⊥DF,故有DF⊥面OMP,所以OM⊥DF,由此可证得∠OMP即二面角的平面角,
在直线三角形DOA中,由于OA=OD,故P是AD中点,易得OP=1
在直角三角形DAF中可求得DF=
| 6 |
由于△DAF≈△DMP,故有
| DP |
| DF |
| MP |
| AF |
| DP×AF |
| DF |
1×
| ||
|
| ||
| 3 |
在直角三角形OPM中,tan∠OMP=
| OP |
| MP |
| 1 | ||||
|
| 3 |
二面角A-DF-B的大小为60°
点评:本题考查线面垂直的证明以及二面角的求法,对于求二面角,要注意其步骤为作角,证角,求角三步,尤其是第二步,证角易漏掉,做题时要切记.

练习册系列答案
相关题目
 如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,CD=2AB=2AD.
如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,CD=2AB=2AD. 如图所示,直线AB的方程为6x-3y-4=0,向边长为2的正方形内随机地投飞镖,飞镖都能投入正方形内,且投到每个点的可能性相等,则飞镖落在阴影部分(三角形ABC的内部)的概率是( )
如图所示,直线AB的方程为6x-3y-4=0,向边长为2的正方形内随机地投飞镖,飞镖都能投入正方形内,且投到每个点的可能性相等,则飞镖落在阴影部分(三角形ABC的内部)的概率是( ) (2012•金华模拟)如图所示的正方形中,将边AB、AD各4等分,分别作AB、AD的平行线段成4×4方格网,则从图中取出一由网格线形成的矩形,恰好为正方形的概率是
(2012•金华模拟)如图所示的正方形中,将边AB、AD各4等分,分别作AB、AD的平行线段成4×4方格网,则从图中取出一由网格线形成的矩形,恰好为正方形的概率是 如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点.
如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点.