题目内容
我校高一年级研究性学习小组共有9名学生,其中有3名男生和6名女生.在研究学习过程中,要进行两次汇报活动(即开题汇报和结题汇报),每次汇报都从这9名学生中随机选1人作为代表发言.设每人每次被选中与否均互不影响.(Ⅰ)求两次汇报活动都由小组成员甲发言的概率;
(Ⅱ)设ξ为男生发言次数与女生发言次数之差的绝对值,求ξ的分布列和数学期望.
【答案】分析:(1)由每人每次被选中与否均互不影响知本题是一个相互独立事件同时发生的概率.事件包含第一次汇报由甲发言且第二次回报也由乙发言,根据相互独立事件同时发生的概率得到结果.
(2)由题意知ξ为男生发言次数与女生发言次数之差的绝对值,当都是男生或都是女生发言时,变量是2,当女生和男生各有一个人时,变量是0,根据变量的意义求出概率,写出分布列和期望.
解答:解:(Ⅰ)解:由每人每次被选中与否均互不影响知本题是一个相互独立事件同时发生的概率.
记“2次汇报活动都是由小组成员甲发言”为事件A.
事件A包含第一次汇报由甲发言且第二次回报也由乙发言,
由题意得事件A的概率P(A)=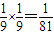 ,
,
即2次汇报活动都是由小组成员甲发言的概率为 .
.
(Ⅱ)解:由题意,ξ的可能取值为2,0,
∵每次汇报时,男生被选为代表的概率为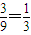 ,女生被选为代表的概率为1-
,女生被选为代表的概率为1- =
= .
.
P(ξ=2)=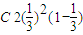 +
+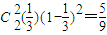 ;
;
P(ξ=0)=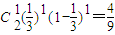 ;
;
∴ξ的分布列为:

∴ξ的数学期望Eξ=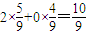 .
.
点评:本题考查离散型随机变量的分布列和期望,这种类型是近几年高考题中经常出现的,考查离散型随机变量的分布列和期望,大型考试中理科考试必出的一道问题.
(2)由题意知ξ为男生发言次数与女生发言次数之差的绝对值,当都是男生或都是女生发言时,变量是2,当女生和男生各有一个人时,变量是0,根据变量的意义求出概率,写出分布列和期望.
解答:解:(Ⅰ)解:由每人每次被选中与否均互不影响知本题是一个相互独立事件同时发生的概率.
记“2次汇报活动都是由小组成员甲发言”为事件A.
事件A包含第一次汇报由甲发言且第二次回报也由乙发言,
由题意得事件A的概率P(A)=
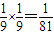 ,
,即2次汇报活动都是由小组成员甲发言的概率为
 .
.(Ⅱ)解:由题意,ξ的可能取值为2,0,
∵每次汇报时,男生被选为代表的概率为
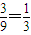 ,女生被选为代表的概率为1-
,女生被选为代表的概率为1- =
= .
.P(ξ=2)=
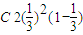 +
+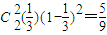 ;
;P(ξ=0)=
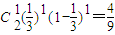 ;
;∴ξ的分布列为:

∴ξ的数学期望Eξ=
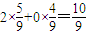 .
.点评:本题考查离散型随机变量的分布列和期望,这种类型是近几年高考题中经常出现的,考查离散型随机变量的分布列和期望,大型考试中理科考试必出的一道问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目