题目内容
某电器商经过多年的经验发现本店每个月售出的电冰箱的台数ξ是一个随机变量，它的分布列为：P（ξ=i）=
（i=1，2，…，12）；设每售出一台电冰箱，电器商获利300元．如销售不出，则每台每月需花保管费100元．问电器商每月初购进多少台电冰箱才能使月平均收益最大？
| 1 |
| 12 |
设x为电器商每月初购进的冰箱的台数，依题意，只需考虑1≤x≤12的情况．
设电器商每月的收益为y
则y是随机变量ξ的函数，且y=
于是电器商每月获益的平均数，即为数学期望
Ey=300x（Px+Px+1+…+P12）+[300-100（x-1）]P1+[2×300-100（x-2）]P2+…+[（x-1）×300-100]Px-1
=300x(12-x+1)•
+
[300•
-100•
]=
(-2x2+38x)．
∵x∈N*，
∴当x=9或x=10时，数学期望最大．
设电器商每月的收益为y
则y是随机变量ξ的函数，且y=
|
于是电器商每月获益的平均数，即为数学期望
Ey=300x（Px+Px+1+…+P12）+[300-100（x-1）]P1+[2×300-100（x-2）]P2+…+[（x-1）×300-100]Px-1
=300x(12-x+1)•
| 1 |
| 12 |
| 1 |
| 12 |
| x(x-1) |
| 2 |
| (x-1)x |
| 2 |
| 25 |
| 3 |
∵x∈N*，
∴当x=9或x=10时，数学期望最大．
练习册系列答案
相关题目
是一个随机变量，它的
；设每售出一台电冰箱，电器商获利300元.
(k=1,2,…,12).设每售出一台电冰箱该经销商获利300元，如果销售不出而囤积于仓库，则每台每月需支付保养费100元，问该电器商月初购进多少台电冰箱才能使自己月平均收益最大？ 某电器商经过多年的经验发现本店每个月售出的电冰箱的台数
是一个随机变量，它的分布列如下：
|
| 1 | 2 | 3 | …… | 12 |
| P |
|
|
| …… |
|
设每售出一台电冰箱，电器商获利300元。如销售不出而囤积于仓库，则每台每月需花保养费100元。问电器商每月初购进多少台电冰箱才能使自己月平均收益最大？
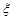是一个随机变量，它的分布列为：
；设每售出一台电冰箱，电器商获利300元.如销售不出，则每台每月需花保管费100元. 问电器商每月初购进多少台电冰箱才能使月平均收益最大？