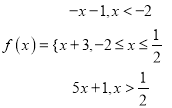Question

【题目】下列命题中的假命题是(　　)

A. α，β∈R，使sin(α＋β)＝sinα＋sinβ

B. φ∈R，函数f(x)＝sin(2x＋φ)都不是偶函数

C. x0∈R，使 (a，b，c∈R且为常数)

D. a>0，函数f(x)＝ln2x＋lnx－a有零点

Answer 1

【答案】B

【解析】取α＝0时，sin(α＋β)＝sinα＋sinβ，A正确；

取时，函数是偶函数，B错误；

对于三次函数f(x)＝x3＋ax2＋bx＋c，当x→－∞时，y→－∞，当x→＋∞时，y→＋∞，又f(x)在R上为连续函数，故x0∈R，使，C正确；

当f(x)＝0时，ln2x＋lnx－a＝0，则有，所以a>0，函数f(x)＝ln2x＋lnx－a＝0有零点，D正确．

本题选择B选项.