题目内容
下列命题中,真命题是( )
| A、?x0∈R,ex0≤0 | ||||||||||||||||
| B、?x∈R,2x>x2 | ||||||||||||||||
| C、“a>1,b>1”是“ab>1”的充分不必要条件 | ||||||||||||||||
D、设
|
分析:根据含有量词的命题的定义以及充分条件和必要条件的定义分别进行判断即可.
解答:解:A.?x∈R,ex>0,∴A错误.
B.当x=-1时,2x>x2不成立.
C.当a>1,b>1时,ab>1成立,但当a=-2,b=-2时满足ab>1但a>1,b>1不成立.∴“a>1,b>1”是“ab>1”的充分不必要条件,正确.
D.由|
•
|=|
||
|得|
•
|=|
||
|cos<
,
>=|
||
|,∴cos<
,
>=1,即<
,
>=0,此时
∥
成立,∴充分性成立,即D错误.
故选:C.
B.当x=-1时,2x>x2不成立.
C.当a>1,b>1时,ab>1成立,但当a=-2,b=-2时满足ab>1但a>1,b>1不成立.∴“a>1,b>1”是“ab>1”的充分不必要条件,正确.
D.由|
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
故选:C.
点评:本题主要考查含有量词的命题的判断,以及充分条件和必要条件的应用,根据定义是解决本题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
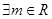 ,使函数
,使函数 是偶函数
是偶函数 ,使函数
,使函数 ≤0
≤0 =-1
=-1