题目内容
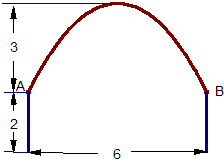 一条隧道的横断面由抛物线弧及一个矩形的三边围成,尺寸如图所示(单位:m),一辆卡车空车时能通过此隧道,现载一集装箱,箱宽3m,车与箱共高4.5m,此车是否能通过隧道?并说明理由.
一条隧道的横断面由抛物线弧及一个矩形的三边围成,尺寸如图所示(单位:m),一辆卡车空车时能通过此隧道,现载一集装箱,箱宽3m,车与箱共高4.5m,此车是否能通过隧道?并说明理由.分析:建立直角坐标系,得到A、B的坐标,设抛物线方程为x2=-2py(p>0),并求得其方程,依题意,集装箱上表面距抛物线型隧道拱顶0.5m,从而设抛物线上点D的坐标为(x0,-0.5),计算即可判断.
解答:解:如图,建立坐标系,则A(-3,-3),B(3,-3).
设抛物线方程为x2=-2py(p>0),
将B点坐标代入,得9=-2p•(-3),
∴p=
.
∴抛物线方程为x2=-3y(-3≤y≤0).
∵车与箱共高4.5m
∴集装箱上表面距抛物线型隧道拱顶0.5m.
设抛物线上点D的坐标为(x0,-0.5),则x02=
,
∴x0=±
=±
,
∴|DD′|=2|x0|=
<3,故此车不能通过隧道.
设抛物线方程为x2=-2py(p>0),
将B点坐标代入,得9=-2p•(-3),
∴p=
| 3 |
| 2 |
∴抛物线方程为x2=-3y(-3≤y≤0).
∵车与箱共高4.5m
∴集装箱上表面距抛物线型隧道拱顶0.5m.
设抛物线上点D的坐标为(x0,-0.5),则x02=
| 3 |
| 2 |
∴x0=±
|
| ||
| 2 |
∴|DD′|=2|x0|=
| 6 |
点评:本题考查抛物线的简单性质,求得抛物线方程是关键,考查分析推理与运算能力,属于中档题.

练习册系列答案
相关题目
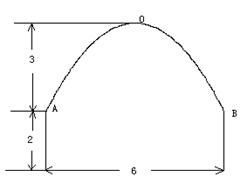
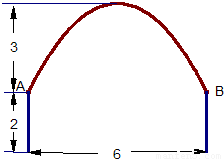 一条隧道的横断面由抛物线弧及一个矩形的三边围成,尺寸如图所示(单位:m),一辆卡车空车时能通过此隧道,现载一集装箱,箱宽3m,车与箱共高4.5m,此车是否能通过隧道?并说明理由.
一条隧道的横断面由抛物线弧及一个矩形的三边围成,尺寸如图所示(单位:m),一辆卡车空车时能通过此隧道,现载一集装箱,箱宽3m,车与箱共高4.5m,此车是否能通过隧道?并说明理由.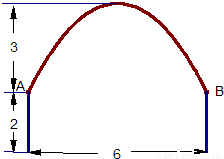 一条隧道的横断面由抛物线弧及一个矩形的三边围成,尺寸如图所示(单位:m),一辆卡车空车时能通过此隧道,现载一集装箱,箱宽3m,车与箱共高4.5m,此车是否能通过隧道?并说明理由.
一条隧道的横断面由抛物线弧及一个矩形的三边围成,尺寸如图所示(单位:m),一辆卡车空车时能通过此隧道,现载一集装箱,箱宽3m,车与箱共高4.5m,此车是否能通过隧道?并说明理由.