题目内容
已知函数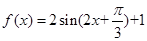 .
.
(Ⅰ)当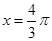 时,求
时,求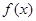 值;
值;
(Ⅱ)若存在区间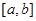 (
(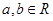 且
且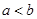 ),使得
),使得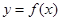 在
在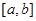 上至少含有6个零
上至少含有6个零
点,在满足上述条件的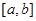 中,求
中,求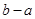 的最小值.
的最小值.
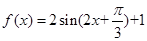 .
.(Ⅰ)当
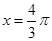 时,求
时,求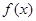 值;
值;(Ⅱ)若存在区间
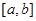 (
(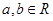 且
且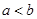 ),使得
),使得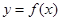 在
在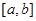 上至少含有6个零
上至少含有6个零点,在满足上述条件的
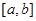 中,求
中,求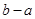 的最小值.
的最小值.(Ⅰ)1;(Ⅱ)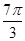
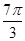
试题分析:(Ⅰ)将
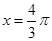 代入函数利用诱导公式和特殊角三角函数值求
代入函数利用诱导公式和特殊角三角函数值求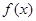 值。(Ⅱ)
值。(Ⅱ)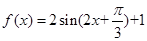 周期为
周期为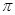 ,此函数在一个周期内含两个零点,所以至少6个零点需要至少3个周期,应先求第一个周期上的两个零点,再根据周期求第一周期的后一个零点和第二个周期的第一个零的距离,从而求出相邻3个零点的两段间隔。画图利用数形结合分析即可求
,此函数在一个周期内含两个零点,所以至少6个零点需要至少3个周期,应先求第一个周期上的两个零点,再根据周期求第一周期的后一个零点和第二个周期的第一个零的距离,从而求出相邻3个零点的两段间隔。画图利用数形结合分析即可求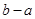 最小值。
最小值。 试题解析:解:(1)当
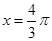 时,
时,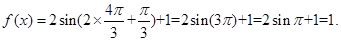 4分
4分(2)
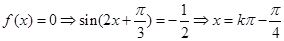 或
或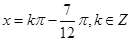 ,即
,即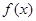 的零点相离间隔依次为
的零点相离间隔依次为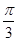 和
和 , 7分
, 7分故若
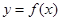 在
在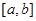 上至少含有6个零点,则
上至少含有6个零点,则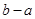 的最小值为
的最小值为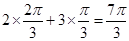 . 9分
. 9分 
练习册系列答案
相关题目
 .
. 的值;
的值; 的值.
的值. cos
cos ,x∈R
,x∈R 的值;
的值; ,θ∈
,θ∈ ,求f
,求f .
. 是
是 的一个内角,且
的一个内角,且 ,则
,则 的值为( )
的值为( )







 ,则
,则 ( )
( )



 ,则
,则 的值为________.
的值为________. 是第二象限的角,且
是第二象限的角,且 ,则
,则 的值为 .
的值为 . 则
则 ( )
( )