题目内容
已知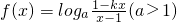 是奇函数
是奇函数
(Ⅰ)求k的值,并求该函数的定义域;
(Ⅱ)根据(Ⅰ)的结果,判断f(x)在(1,+∞)上的单调性,并给出证明.
解:(Ⅰ)∵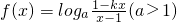 是奇函数,
是奇函数,
∴f(x)+f(-x)=0,即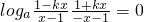
则1-k2x2=1-x2,即k=±1,
当k=1时, ,所以k=-1
,所以k=-1
定义域为:{x|x>1或x<-1}
(Ⅱ)在(1,+∞)上任取x1,x2,并且x1>x2,则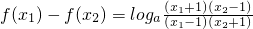
又(x1+1)(x2-1)-(x1-1)(x2+1)=2(x2-x1)<0∴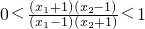 ,又a>1,
,又a>1,
∴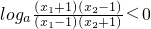
所以f(x1)<f(x2),所以f(x)在(1,+∞)上是单调递减函数
分析:(I)根据函数是奇函数,则f(x)+f(-x)=0,建立等式关系,求出k的值,然后根据真数大于零求出函数的定义域;
(II)在(1,+∞)上任取x1,x2,并且x1>x2,然后判定f(x1)与f(x2)的大小,从而判断f(x)在(1,+∞)上的单调性.
点评:本题主要考查了奇函数的定义,以及函数的定义域和函数在给定区间上的单调性,同时考查了计算能力,属于中档题.
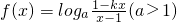 是奇函数,
是奇函数,∴f(x)+f(-x)=0,即
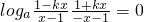
则1-k2x2=1-x2,即k=±1,
当k=1时,
 ,所以k=-1
,所以k=-1定义域为:{x|x>1或x<-1}
(Ⅱ)在(1,+∞)上任取x1,x2,并且x1>x2,则
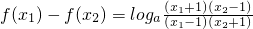
又(x1+1)(x2-1)-(x1-1)(x2+1)=2(x2-x1)<0∴
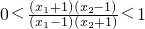 ,又a>1,
,又a>1,∴
所以f(x1)<f(x2),所以f(x)在(1,+∞)上是单调递减函数
分析:(I)根据函数是奇函数,则f(x)+f(-x)=0,建立等式关系,求出k的值,然后根据真数大于零求出函数的定义域;
(II)在(1,+∞)上任取x1,x2,并且x1>x2,然后判定f(x1)与f(x2)的大小,从而判断f(x)在(1,+∞)上的单调性.
点评:本题主要考查了奇函数的定义,以及函数的定义域和函数在给定区间上的单调性,同时考查了计算能力,属于中档题.

练习册系列答案
相关题目
 ,已知
,已知 是奇函数。
是奇函数。 、
、 的值。
的值。 的单调区间与极值。
的单调区间与极值。 ,已知
,已知 是奇函数。
是奇函数。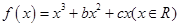 ,已知
,已知 是奇函数。
是奇函数。 、
、 的值。
的值。 的单调区间与极值。
的单调区间与极值。