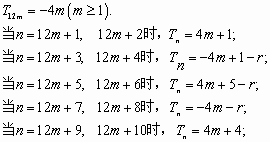题目内容
已知数列{an}:a1=1,a2=2,a3=r,an+3=an+2(n是正整数),与数列{bn}:b1=1,b2=0,b3=-1,b4=0,bn+4=bn(n是正整数).
记Tn=b1a1+b2a2+b3a3+…+bnan.
(1)若a1+a2+a3+…+a12=64,求r的值;
(2)求证:当n是正整数时,T12n=-4n;
(3)已知r>0,且存在正整数m,使得在T12n+1,T12m+2,…,T12m+12中有4项为100.求r的值,并指出哪4项为100.
答案:
解析:
解析:
|
[解](1) ∵ [证明](2)用数学归纳法证明:当 ①当n=1时, ②假设n=k时等式成立,即 那么当 根据①和②可以断定:当 [解](3) ∵4m+1是奇数, ∴这些项均不可能取到100. 15分 此时, |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目