题目内容
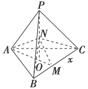
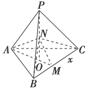
如图所示,三棱锥P-ABC中,PA⊥平面ABC,∠BAC=60°,PA=AB=AC=2,E是PC的中点.(1)(文)求证AE与PB是异面直线.
(理)求异面直线AE和PB所成角的余弦值;
(2)求三棱锥A-EBC的体积.

【答案】分析:(1)(文)假设AE与PB共面,设平面为α,用反证法证明,推出矛盾这与P∉平面ABE矛盾,即可证明AE与PB是异面直线.
(理)取BC的中点F,连接EF、AF,则EF∥PB,说明∠AEF或其补角就是异面直线AE和PB所成角,解三角形求异面直线AE和PB所成角的余弦值;
(2)求出底面ABC的面积,求出E到平面ABC的距离,即可求三棱锥A-EBC的体积.
解答: 解:(1)(文)证明:假设AE与PB共面,设平面为α,
解:(1)(文)证明:假设AE与PB共面,设平面为α,
∵A∈α,B∈α,E∈α,
∴平面α即为平面ABE,
∴P∈平面ABE,
这与P∉平面ABE矛盾,
所以AE与PB是异面直线.
(理)取BC的中点F,连接EF、AF,则EF∥PB,所以∠AEF或其补角就是异面直线AE和PB所成角.
∵∠BAC=60°,PA=AB=AC=2,PA⊥平面ABC,
∴AF= ,AE=
,AE= ,EF=
,EF= ;
;
cos∠AEF= =
= ,
,
所以异面直线AE和PB所成角的余弦值为 .
.
(2)因为E是PC中点,所以E到平面ABC的距离为 PA=1,
PA=1,
VA-EBC=VE-ABC= ×(
×( ×2×2×
×2×2× )×1=
)×1= .
.
点评:本题考查异面直线的判定,棱柱、棱锥、棱台的体积,异面直线及其所成的角,考查空间想象能力,逻辑思维能力,是中档题,常考题型.
(理)取BC的中点F,连接EF、AF,则EF∥PB,说明∠AEF或其补角就是异面直线AE和PB所成角,解三角形求异面直线AE和PB所成角的余弦值;
(2)求出底面ABC的面积,求出E到平面ABC的距离,即可求三棱锥A-EBC的体积.
解答:
 解:(1)(文)证明:假设AE与PB共面,设平面为α,
解:(1)(文)证明:假设AE与PB共面,设平面为α,∵A∈α,B∈α,E∈α,
∴平面α即为平面ABE,
∴P∈平面ABE,
这与P∉平面ABE矛盾,
所以AE与PB是异面直线.
(理)取BC的中点F,连接EF、AF,则EF∥PB,所以∠AEF或其补角就是异面直线AE和PB所成角.
∵∠BAC=60°,PA=AB=AC=2,PA⊥平面ABC,
∴AF=
 ,AE=
,AE= ,EF=
,EF= ;
;cos∠AEF=
 =
= ,
,所以异面直线AE和PB所成角的余弦值为
 .
.(2)因为E是PC中点,所以E到平面ABC的距离为
 PA=1,
PA=1,VA-EBC=VE-ABC=
 ×(
×( ×2×2×
×2×2× )×1=
)×1= .
.点评:本题考查异面直线的判定,棱柱、棱锥、棱台的体积,异面直线及其所成的角,考查空间想象能力,逻辑思维能力,是中档题,常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
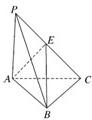 如图所示,三棱锥P-ABC中,PA⊥平面ABC,∠BAC=60°,PA=AB=AC=2,E是PC的中点.
如图所示,三棱锥P-ABC中,PA⊥平面ABC,∠BAC=60°,PA=AB=AC=2,E是PC的中点.