题目内容
已知圆O的方程为 ,圆M的方程为
,圆M的方程为 ,过圆M上任意一点P作圆O的切线PA,若直线PA与圆M的另一个交点为Q,则当PQ的长度最大时,直线PA的斜率是___________.
,过圆M上任意一点P作圆O的切线PA,若直线PA与圆M的另一个交点为Q,则当PQ的长度最大时,直线PA的斜率是___________.
1或-7
解析试题分析:根据题意可以分析圆O的圆心到PA的距离为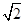 ,那么可知要使得在直角三角形QPA中,PQ最大,则只要OQ最大即可,那么即圆O的圆心到圆M上点的距离的最大值问题来处理,由于点|OM|为定值,且为
,那么可知要使得在直角三角形QPA中,PQ最大,则只要OQ最大即可,那么即圆O的圆心到圆M上点的距离的最大值问题来处理,由于点|OM|为定值,且为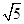 ,那么可知连接OM,则PA的长度结合勾股定理可知。那么设直线PA的斜率为k,那么PQ的中点与点M的连线的斜率为
,那么可知连接OM,则PA的长度结合勾股定理可知。那么设直线PA的斜率为k,那么PQ的中点与点M的连线的斜率为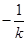 ,那么联立方程组可知其斜率为1或-7。
,那么联立方程组可知其斜率为1或-7。
考点:本试题考查了圆内弦的长度问题。
点评:要分析圆内弦的最值问题,可以结合圆的半径和弦心距,以及半弦长的关系来分析,这是解决该试题的关键,同时要利用两圆的位置关系,要使得PQ最大,只要点M到PA的距离最小即可。转化为点到直线的距离的最小值来进行,进而求得斜率值,属于中档题。

练习册系列答案
相关题目
 ,若以坐标原点
,若以坐标原点 为极点,
为极点,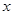 轴的正半轴为极轴,则该圆的极坐标方程可写为 .
轴的正半轴为极轴,则该圆的极坐标方程可写为 . (
( 是实数)与圆
是实数)与圆 相交于
相交于 两点,且
两点,且 (
( 是坐标原点)是直角三角形,则点
是坐标原点)是直角三角形,则点 与点
与点 之间距离的最小值是 .
之间距离的最小值是 . 与圆
与圆 关于直线
关于直线 对称,则
对称,则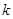 为何实数,直线
为何实数,直线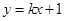 与曲线
与曲线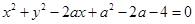 恒有交点,则实数
恒有交点,则实数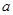 的取值范围为 。
的取值范围为 。 作一动直线交圆C于两点A、B,过坐标原点O作直线ON⊥AM于点N,过点A的切线交直线ON于点Q,则
作一动直线交圆C于两点A、B,过坐标原点O作直线ON⊥AM于点N,过点A的切线交直线ON于点Q,则 = (用R表示)
= (用R表示) 关于
关于 轴对称的圆的方程为______________.
轴对称的圆的方程为______________. 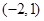 发出的一束光线,经
发出的一束光线,经 轴反射后,反射光线恰好平分圆:
轴反射后,反射光线恰好平分圆:
 的圆周,则反射光线所在的直线方程为 .
的圆周,则反射光线所在的直线方程为 . 的圆心位于第三象限,则直线
的圆心位于第三象限,则直线 一定不经过第_______象限.
一定不经过第_______象限.