题目内容
(1)已知M={(x,y)|y=x+a},N={(x,y)|x2+y2=2}求使等式M∩N=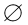 成立的实数a的范围.
成立的实数a的范围.
(2)设A={-3,4},B={x|x2-2ax+b=0},B≠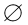 且A∩B=B,求a,b的值.
且A∩B=B,求a,b的值.
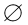 成立的实数a的范围.
成立的实数a的范围.(2)设A={-3,4},B={x|x2-2ax+b=0},B≠
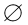 且A∩B=B,求a,b的值.
且A∩B=B,求a,b的值. 解:(1)∵M={(x,y)|y=x+a},N={(x,y)|x2+y2=2}
又∵M∩N=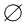
∴y=x+a与x2+y2=2没有交点即2x2+2ax+a2﹣2=0没有解
∴△=4a2﹣8(a2﹣2)<0
∴a>2或a<﹣2
(2)∵A∩B=B,A={﹣3,4},B≠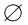
∴B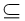 A ∴B={﹣3}或B={4}或B={﹣3,4}
A ∴B={﹣3}或B={4}或B={﹣3,4}
①当B={﹣3}时,则方程x2﹣2ax+b=0只有一个根﹣3
∴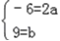 ∴a=﹣3,b=9
∴a=﹣3,b=9
②当B={4}时,则方程x2﹣2ax+b=0只有一个根4
∴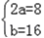 ∴a=4,b=16
∴a=4,b=16
③当B={﹣3,4}时,则方程x2﹣2ax+b=0有两个根﹣3,4
∴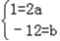 ∴a=
∴a= ,b=﹣12
,b=﹣12
又∵M∩N=
∴y=x+a与x2+y2=2没有交点即2x2+2ax+a2﹣2=0没有解
∴△=4a2﹣8(a2﹣2)<0
∴a>2或a<﹣2
(2)∵A∩B=B,A={﹣3,4},B≠
∴B
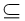 A ∴B={﹣3}或B={4}或B={﹣3,4}
A ∴B={﹣3}或B={4}或B={﹣3,4}①当B={﹣3}时,则方程x2﹣2ax+b=0只有一个根﹣3
∴
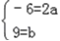 ∴a=﹣3,b=9
∴a=﹣3,b=9②当B={4}时,则方程x2﹣2ax+b=0只有一个根4
∴
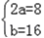 ∴a=4,b=16
∴a=4,b=16 ③当B={﹣3,4}时,则方程x2﹣2ax+b=0有两个根﹣3,4
∴
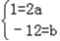 ∴a=
∴a= ,b=﹣12
,b=﹣12 
练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目