题目内容
15.已知直线l:y=kx+1,椭圆C:x2+$\frac{{y}^{2}}{4}$=1.(1)求证:直线1与椭圆C有两个交点;
(2)若k=2,求直线l被椭圆C截得的弦长.
分析 (1)直接联立直线方程与椭圆方程,由判别式大于0证得结论;
(2)把k=2代入(1)中的方程,利用根与系数的关系得到直线l被椭圆C截得的弦的两个端点的横坐标的和与积,代入弦长公式得答案.
解答 (1)证明:联立$\left\{\begin{array}{l}{y=kx+1}\\{{x}^{2}+\frac{{y}^{2}}{4}=1}\end{array}\right.$,得(4+k2)x2+2kx-3=0 ①.
∵△=(2k)2-4×(4+k2)×(-3)=16k2+48>0,
∴直线1与椭圆C有两个交点;
(2)解:当k=2时,①可化为8x2+4x-3=0,
设直线l被椭圆C截得的线段的两端点为A(x1,y1),B(x2,y2),
则${x}_{1}+{x}_{2}=-\frac{1}{2}$,${x}_{1}{x}_{2}=-\frac{3}{8}$.
∴直线l被椭圆C截得的弦长为|AB|=$\sqrt{1+{k}^{2}}|{x}_{1}-{x}_{2}|$=$\sqrt{1+{2}^{2}}\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$
=$\sqrt{5}\sqrt{(-\frac{1}{2})^{2}+4×\frac{3}{8}}=\frac{\sqrt{35}}{2}$.
点评 本题考查直线与圆锥曲线的位置关系,考查了弦长公式的应用,体现了“设而不求”的解题思想方法,是中档题.

练习册系列答案
相关题目
6.已知$\frac{π}{4}<α<π,cos(α-\frac{π}{4})=\frac{3}{5}$,则tanα=( )
| A. | 7 | B. | 7或$\frac{1}{7}$ | C. | -7 | D. | $-\frac{1}{7}或7$ |
10.下列命题中不正确的是( )
| A. | 向量$\overrightarrow{AB}$与向量$\overrightarrow{BA}$的长度相等 | |
| B. | 任意一个非零向量都可以平行移动 | |
| C. | 若$\overrightarrow{a}$∥$\overrightarrow{b}$,且$\overrightarrow{b}$≠$\overrightarrow{0}$,则$\overrightarrow{a}$≠$\overrightarrow{0}$ | |
| D. | 两个有共同起点且共线的向量,其终点不一定相同. |
7.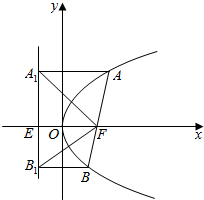 如图所示,线段AB时抛物线的焦点弦,F为抛物线焦点,若A,B在其准线上的射影分别为A1,B1,则∠A1FB1等于( )
如图所示,线段AB时抛物线的焦点弦,F为抛物线焦点,若A,B在其准线上的射影分别为A1,B1,则∠A1FB1等于( )
 如图所示,线段AB时抛物线的焦点弦,F为抛物线焦点,若A,B在其准线上的射影分别为A1,B1,则∠A1FB1等于( )
如图所示,线段AB时抛物线的焦点弦,F为抛物线焦点,若A,B在其准线上的射影分别为A1,B1,则∠A1FB1等于( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
 利用随机模拟方法计算y=x3和x=2以及x轴所围成的图形的面积.
利用随机模拟方法计算y=x3和x=2以及x轴所围成的图形的面积.