题目内容
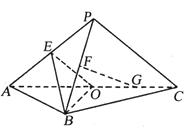
如图所示,四棱锥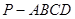 ,底面
,底面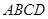 是边长为
是边长为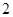 的正方形,
的正方形,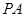 ⊥面
⊥面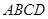 ,
,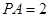 ,过点
,过点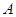 作
作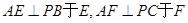 ,连接
,连接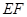 .
.
(Ⅰ)求证: ;
;
(Ⅱ)若面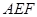 交侧棱
交侧棱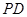 于点
于点 ,求多面体
,求多面体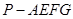 的体积.
的体积.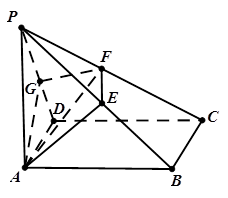
(Ⅰ)略;(Ⅱ)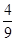 .
.
解析试题分析:(Ⅰ)利用线线垂直证明线面垂直;(Ⅱ)利用椎体体积公式,找高求面积.
试题解析:(Ⅰ)证明: PA⊥面ABCD,BC在面ABCD内,
PA⊥面ABCD,BC在面ABCD内,
∴ PA⊥BC BA⊥BC,PA∩BA=A,∴BC⊥面PAB,
又∵AE在面PAB内∴ BC⊥AE AE⊥PB,BC∩PB="B,"
AE⊥PB,BC∩PB="B,"
∴AE⊥面PBC又∵PC在面PBC内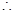 AE⊥PC,
AE⊥PC, 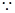 AF⊥PC, AE∩AF="A,"
AF⊥PC, AE∩AF="A,"
∴PC⊥面AEF 6分
(Ⅱ) PC⊥面AEF, ∴ AG⊥PC, 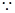 AG⊥DC ∴PC∩DC=C AG⊥面PDC,
AG⊥DC ∴PC∩DC=C AG⊥面PDC,
∵GF在面PDC内∴AG⊥GF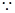 △AGF是直角三角形,
△AGF是直角三角形,
由(1)可知△AEF是直角三角形,AE=AG=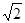 ,EF=GF=
,EF=GF=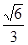 ∴
∴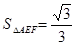 ,
, 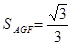 又AF=
又AF=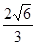 ,∴
,∴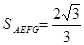 , PF=
, PF=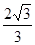
∴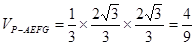 13分
13分
考点:线面垂直的证明,体积求解.

练习册系列答案
相关题目
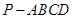 的底面为平行四边形,
的底面为平行四边形,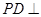 平面
平面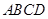 ,
,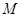 为
为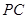 中点.
中点.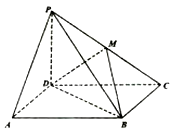
 平面
平面 ;
;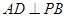 ,求证:
,求证: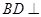 平面
平面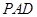 .
.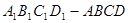 中,
中, ,
,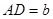 ,
,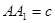 ,
, 是线段
是线段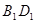 的中点.
的中点.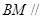 平面
平面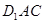 ;
;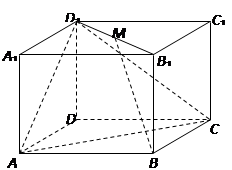
 中,AD//BC,
中,AD//BC,  =900,BA="BC" 把ΔBAC沿
=900,BA="BC" 把ΔBAC沿 折起到
折起到 的位置,使得点
的位置,使得点 在平面ADC上的正投影O恰好落在线段
在平面ADC上的正投影O恰好落在线段 分别为线段PC,CD的中点.
分别为线段PC,CD的中点.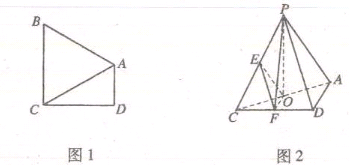
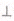 与平面POF;
与平面POF;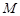 ,使得
,使得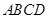 中,
中, 是
是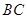 的中点,
的中点, ,
,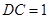 ,
,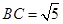 ,
,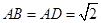 ,将左图沿直线
,将左图沿直线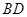 折起,使得二面角
折起,使得二面角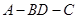 为
为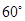 ,如右图.
,如右图.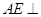 平面
平面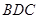 ;
;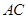 与平面
与平面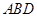 所成角的余弦值.
所成角的余弦值.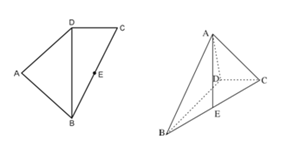
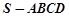 中,底面
中,底面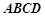 是直角梯形,
是直角梯形, ∥
∥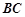 ,
,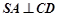 ,
,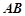 ⊥平面SAD,点
⊥平面SAD,点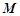 是
是 的中点,且
的中点,且 ,
, .
. 
 ∥平面
∥平面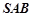 ;
;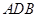 是圆
是圆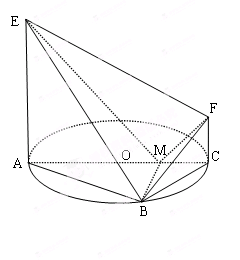
 平面
平面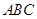 ,
, 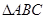 是以
是以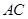 为斜边的等腰直角三角形,
为斜边的等腰直角三角形, 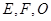 分别为
分别为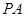 ,
, 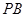 ,
, 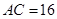 ,
, 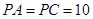 .
.
 是
是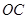 的中点, 证明:
的中点, 证明: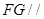 平面
平面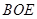 ;
;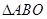 内存在一点
内存在一点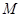 , 使
, 使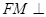 平面
平面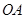 ,
, 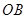 的距离.
的距离.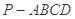 中,底面
中,底面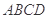 为正方形,
为正方形,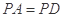
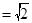 ,
,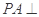 平面
平面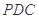 ,
, 为棱
为棱 的中点.
的中点.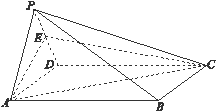
 平面
平面 ;
; 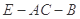 的余弦值.
的余弦值. 到平面
到平面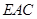 的距离.
的距离.