题目内容
如图1,在直角梯形 中,AD//BC,
中,AD//BC, 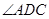 =900,BA="BC" 把ΔBAC沿
=900,BA="BC" 把ΔBAC沿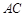 折起到
折起到 的位置,使得点
的位置,使得点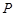 在平面ADC上的正投影O恰好落在线段
在平面ADC上的正投影O恰好落在线段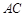 上,如图2所示,点
上,如图2所示,点 分别为线段PC,CD的中点.
分别为线段PC,CD的中点.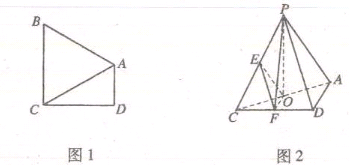
(I) 求证:平面OEF//平面APD;
(II)求直线CD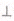 与平面POF;
与平面POF;
(III)在棱PC上是否存在一点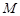 ,使得
,使得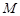 到点P,O,C,F四点的距离相等?请说明理由.
到点P,O,C,F四点的距离相等?请说明理由.
(I) (II)详见解析; (III)存在点M满足条件.
解析试题分析:(I) 要证平面OEF//平面APD ,只需借助所给中点,证明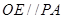 、
、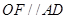 即可; (II) 借助底面为直角梯形及
即可; (II) 借助底面为直角梯形及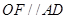 可得
可得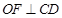 ,另由已知可得:
,另由已知可得: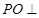 平面
平面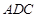 ,进而可得
,进而可得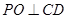 ,从而可证
,从而可证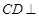 平面
平面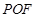 ;(III)记点
;(III)记点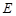 为
为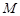 ,证明即可.
,证明即可.
试题解析:(I)因为点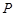 在平面
在平面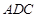 上的正投影
上的正投影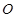 恰好落在线段
恰好落在线段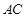 上
上
所以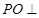 平面
平面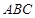 ,所以
,所以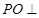
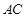 2分
2分
因为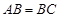 ,
,
所以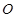 是
是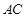 中点, 3分
中点, 3分
所以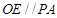 4分
4分
同理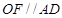
又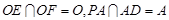
所以平面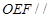 平面
平面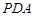 ; 6分
; 6分
(II)因为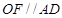 ,
,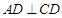
所以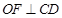 7分
7分
又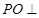 平面
平面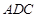 ,
, 平面
平面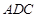
所以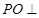
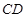 8分
8分
又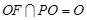
所以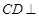 平面
平面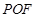 ; 10分
; 10分
(III)存在,事实上记点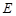 为
为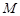 即可 11分
即可 11分
因为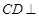 平面
平面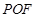 ,
,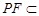 平面
平面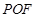
所以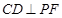
又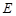 为
为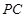 中点,所以
中点,所以  &
&

 学习实践园地系列答案
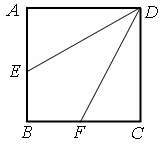
学习实践园地系列答案 中,点
中,点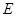 是
是 的中点,点
的中点,点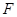 是
是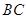 的中点,将△
的中点,将△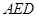 、△
、△ 分别沿
分别沿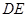 、
、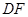 折起,使
折起,使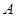 、
、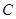 两点重合于点
两点重合于点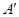 ,连接
,连接 ,
, .
.

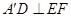 ; (2)求点
; (2)求点 的距离.
的距离. 中,
中, ⊥底面
⊥底面 ,四边形
,四边形 ⊥
⊥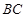 ,
, ,
,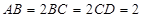 .
.
 ⊥平面
⊥平面 ;
;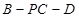 的余弦值为
的余弦值为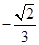 ,求
,求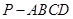 中,
中,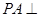 底面
底面 ,四边形
,四边形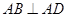 ,
,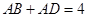 ,
,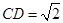 ,
,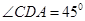 .
.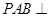 平面
平面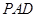 ;
;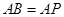 .
.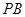 与平面
与平面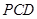 所成的角为
所成的角为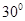 ,求线段
,求线段 的长;
的长;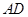 上是否存在一个点
上是否存在一个点 ,使得点
,使得点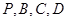 的距离都相等?说明理由.
的距离都相等?说明理由.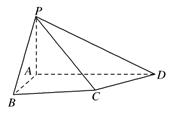
 中,底面
中,底面 是矩形,四条侧棱长均相等.
是矩形,四条侧棱长均相等.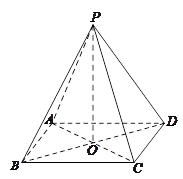
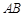
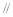 平面
平面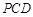 ;
;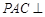 平面
平面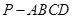 中,
中, 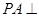 平面
平面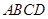 ,
,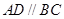 ,
,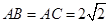 ,
,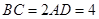 .
. 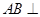 平面
平面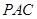 ;
;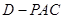 的高.
的高. 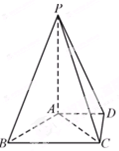
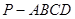 ,底面
,底面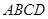 是边长为
是边长为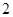 的正方形,
的正方形,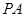 ⊥面
⊥面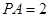 ,过点
,过点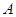 作
作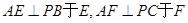 ,连接
,连接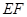 .
. ;
;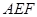 交侧棱
交侧棱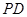 于点
于点 ,求多面体
,求多面体 的体积.
的体积.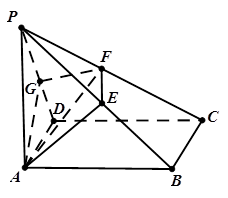
 ,平面
,平面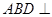 平面
平面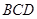 ,AB=AD=1,AB⊥AD,DB=DC,DB⊥DC
,AB=AD=1,AB⊥AD,DB=DC,DB⊥DC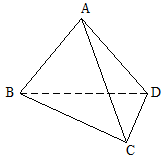
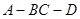 的正切值.
的正切值.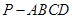 的底面
的底面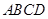 是边长为2的菱形,
是边长为2的菱形,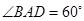 .已知
.已知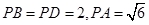 .
.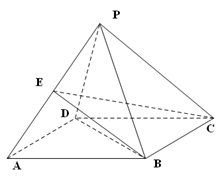
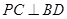
 为
为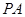 的中点,求三菱锥
的中点,求三菱锥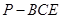 的体积.
的体积.