题目内容
设椭圆M：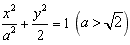
的右焦点为F1，直线l：x=
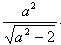与x轴交于点A，若
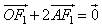（其中O为坐标原点），
（1）求椭圆M的方程；
（2）设P是椭圆M上的任意一点，EF为圆N：x2+（y-2）2=1的任意一条直径（E、F为直径的两个端点），求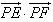
的最大值。
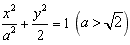的右焦点为F1，直线l：x=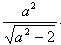与x轴交于点A，若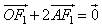（其中O为坐标原点），（1）求椭圆M的方程；
（2）设P是椭圆M上的任意一点，EF为圆N：x2+（y-2）2=1的任意一条直径（E、F为直径的两个端点），求
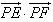的最大值。 解：（1）由题设知，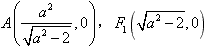
，
由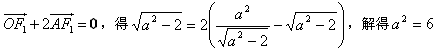
，
所以椭圆的方程M：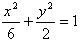
；
（2）设圆N：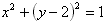
的圆心为N，
则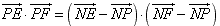
，
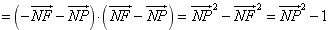从而求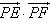
的最大值转化为求
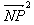的最大值，
因为P是椭圆M上的任意一点，设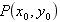
，
所以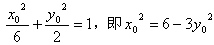
，
因为点N（0，2），
所以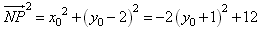
，
因为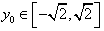
，
所以当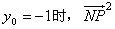
取得最大值12，
所以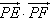
的最大值为11。
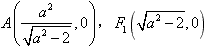，由
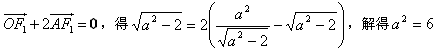，所以椭圆的方程M：
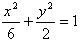；（2）设圆N：
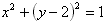的圆心为N，则
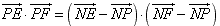
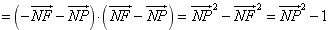，从而求
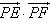的最大值转化为求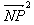的最大值，因为P是椭圆M上的任意一点，设
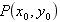，所以
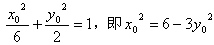，因为点N（0，2），
所以
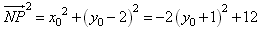，因为
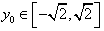，所以当
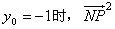取得最大值12，所以
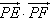的最大值为11。 
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
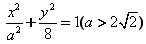的右焦点为F1，直线l：
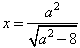与x轴交于点A，若
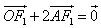（其中O为坐标原点），
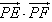的最大值。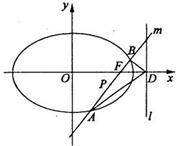 
（
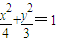）的右焦点为
，过点
的一动直线
绕点
， 
．
为何值时，
MNF为一个正三角形？
的右焦点为F，左顶点为A，点P为曲线D上的动点，以PF为直径的圆恒与y轴相切．
，
））
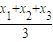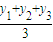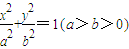的右焦点为F（1，0），短轴的端点分别为B1，B2，且
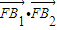=-a．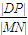
的取值范围．