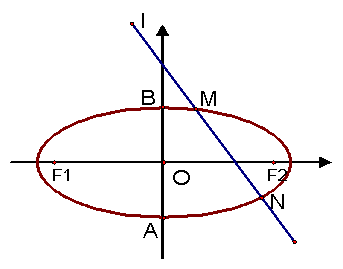
题目内容
如图,椭圆![]() (
(![]() )的右焦点为
)的右焦点为![]() ,过点
,过点![]() 的一动直线
的一动直线![]() 绕点
绕点![]() 转动,并且交椭圆于A,B两点,P为线段AB的中点.
转动,并且交椭圆于A,B两点,P为线段AB的中点.
(1)求点P的轨迹H的方程;
(2)若在Q的方程中,令![]() ,
, ![]() .
.
设轨迹H的最高点和最低点分别为M和N.当![]() 为何值时,
为何值时,![]() MNF为一个正三角形?
MNF为一个正三角形?
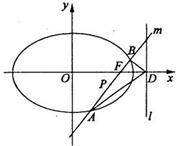
解:如图,(1)设椭圆Q:![]() (a>b>0)
(a>b>0)
上的点A(x1,y1)、B(x2,y2),又设P点坐标为P(x,y),则
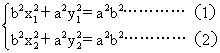
1°当AB不垂直x轴时,x1¹x2,
由(1)-(2)得
b2(x1-x2)2x+a2(y1-y2)2y=0
![]()
b2x2+a2y2-b2cx=0…………(3)
2°当AB垂直于x轴时,点P即为点F,满足方程(3)
故所求点P的轨迹方程为:b2x2+a2y2-b2cx=0
(2)因为轨迹H的方程可化为: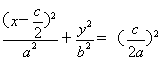
M(![]() ,
,![]() ),N(
),N( ![]() ,-
,-![]() ),F(c,0),使△MNF为一个正三角形时,则
),F(c,0),使△MNF为一个正三角形时,则
tan![]() =
=![]() =
=![]() ,即a2=3b2. 由于
,即a2=3b2. 由于![]() ,
,
![]() ,则1+cosq+sinq=3 sinq,得q=arctan
,则1+cosq+sinq=3 sinq,得q=arctan![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在直角坐标系xOy中,已知椭圆C:
如图,在直角坐标系xOy中,已知椭圆C:

 +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的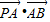 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.