题目内容
已知数列 满足:
满足: ,且对一切
,且对一切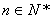 ,有
,有 ,其中
,其中 为数列
为数列 的前
的前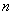 项和.
项和.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)证明: .
.
【答案】
解:
(Ⅰ)法一:归纳得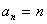 ,然后用数学归纳法证明(略).
,然后用数学归纳法证明(略).
法二:由条件得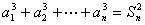 ………①
………①
所以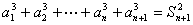 ………②
………②
①—②得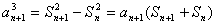 ,则
,则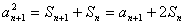 ……………2分
……………2分
所以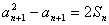 ,又
,又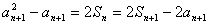 ,
,
所以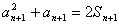 …………③
…………③
则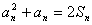 …………④
…………④
③—④得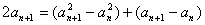 ,从而
,从而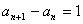 ……………2分
……………2分
又由已知易得 ,所以数列
,所以数列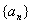 是以首项为
是以首项为 ,公差为1的等差数列
,公差为1的等差数列
所以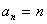 ……………5分
……………5分
(Ⅱ)证明:由第(1)问的解答可知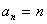 ,则
,则
令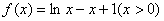 ,则
,则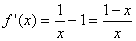
则当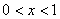 时,
时,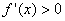 ,所以
,所以 在
在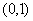 上单调递增;
上单调递增;
当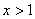 时,
时,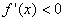 ,所以
,所以 在
在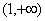 上单调递减
上单调递减
故 在
在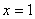 处取得极大值
处取得极大值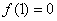
所以当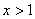 时,
时,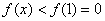 ,即
,即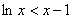 ……………7分
……………7分
则当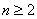 ,
,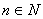 时,
时,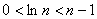 ,则有
,则有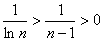
又当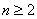 ,
,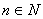 时,恒有
时,恒有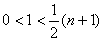 ,则有
,则有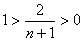
两式相乘有 ……………9分
……………9分
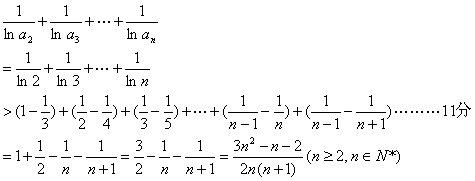 于是
于是
……………12分

练习册系列答案
相关题目
 .
. 满足:
满足: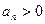 ,且对一切
,且对一切 ,有
,有 ,其中
,其中 为数列
为数列 项和.(Ⅰ)求数列
项和.(Ⅰ)求数列 .
. 满足
满足 ,
, ,且对任意
,且对任意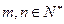 都有
都有
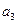 ,
, ;
;
 ,证明:
,证明: 是等差数列;
是等差数列;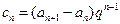
 ,求数列
,求数列 的前n项和
的前n项和 .
. 满足
满足 ,
, ,且对任意
,且对任意 都有
都有
 ,
,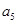 ;
;
 ,证明:
,证明: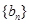 是等差数列;
是等差数列;
 ,求数列
,求数列 的前n项和
的前n项和 .
.