题目内容
已知函数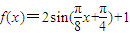 .
.
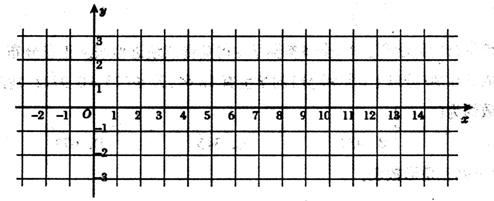
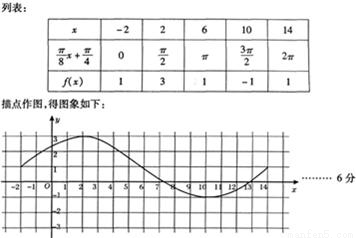
(1)在所给的坐标纸上作出函数y=f(x),x∈[-2,14]的图象(不要求作图过程)
(2)令g(x)=f(x)+f(-x),x∈R,求函数y=g(x)与x轴交点的横坐标.
【答案】分析:(1)用五点法作函数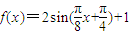 在一个周期[-2,14]上的图象.
在一个周期[-2,14]上的图象.
(2)由条件求出g(x)=2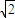 cos
cos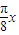 +2,令g(x)=0,可得 cos
+2,令g(x)=0,可得 cos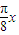 =-
=-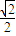 ,由此求得函数y=g(x)与x轴交点的横坐标x的值.
,由此求得函数y=g(x)与x轴交点的横坐标x的值.
解答:解:(1)函数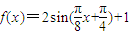 的周期等于16,列表作图如下:
的周期等于16,列表作图如下:
(2)g(x)=f(x)+f(-x)=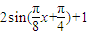 +
+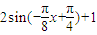
=2sin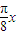 cos
cos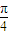 +2cos
+2cos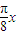 sin
sin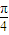 -2sin
-2sin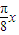 cos
cos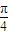 +2cos
+2cos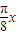 sin
sin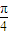 +2=2
+2=2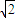 cos
cos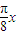 +2,
+2,
由g(x)=0,可得 cos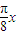 =-
=-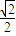 ,故
,故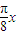 =2kπ±
=2kπ±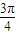 ,k∈z.
,k∈z.
解得 x=16k±6,k∈z.
点评:本题主要考查用五点法作函数y=Asin(ωx+∅)的图象,根据三角函数的值求角的大小,求出g(x)=2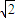 cos
cos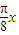 +2,是解题的关键,属于基础题.
+2,是解题的关键,属于基础题.
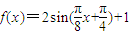 在一个周期[-2,14]上的图象.
在一个周期[-2,14]上的图象.(2)由条件求出g(x)=2
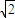 cos
cos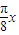 +2,令g(x)=0,可得 cos
+2,令g(x)=0,可得 cos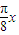 =-
=-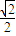 ,由此求得函数y=g(x)与x轴交点的横坐标x的值.
,由此求得函数y=g(x)与x轴交点的横坐标x的值.解答:解:(1)函数
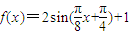 的周期等于16,列表作图如下:
的周期等于16,列表作图如下:
(2)g(x)=f(x)+f(-x)=
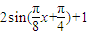 +
+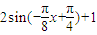
=2sin
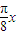 cos
cos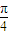 +2cos
+2cos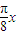 sin
sin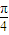 -2sin
-2sin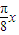 cos
cos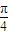 +2cos
+2cos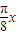 sin
sin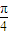 +2=2
+2=2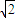 cos
cos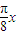 +2,
+2,由g(x)=0,可得 cos
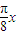 =-
=-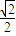 ,故
,故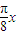 =2kπ±
=2kπ±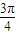 ,k∈z.
,k∈z.解得 x=16k±6,k∈z.
点评:本题主要考查用五点法作函数y=Asin(ωx+∅)的图象,根据三角函数的值求角的大小,求出g(x)=2
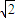 cos
cos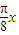 +2,是解题的关键,属于基础题.
+2,是解题的关键,属于基础题. 
练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
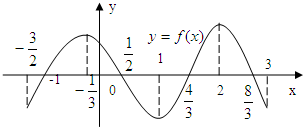 已知函数f(x)在定义域
已知函数f(x)在定义域 已知函数
已知函数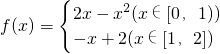 .
.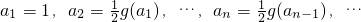 ,求数列{an}的通项公式;
,求数列{an}的通项公式;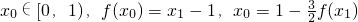 ,求x0和x1的值.
,求x0和x1的值.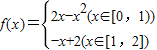 .
.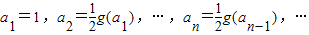 ,求数列{an}的通项公式;
,求数列{an}的通项公式;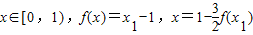 ,求x和x1的值.
,求x和x1的值.
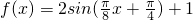 .
.