题目内容
设f(x)=| x |
(1)若F(x)=f(x)+g(x),试求F(x)的单调递减区间;
(2)设G(x)=
|
| 2 |
(3)若不等式|
| f(x)+a[g(x)-2a] |
| f(x) |
分析:(1)先求出F(x)=f(x)+g(x),的解析式,是一个关于
的二次函数,对其配方后再由二次函数的性质研究其单调性,求出单调区间;
(2)根据G(x)的解析式作出图象的示意图,根据几何意义判断出G(x)图象上的点到直线x+y-1=0距离的最小值在点P处取到,由此建立起距离最小值的方程,求出a的值;
(3)不等式|
|≤1对x∈[1,4]恒成立,可通过等价变形逐步探究得出
,解出a的取值范围.
| x |
(2)根据G(x)的解析式作出图象的示意图,根据几何意义判断出G(x)图象上的点到直线x+y-1=0距离的最小值在点P处取到,由此建立起距离最小值的方程,求出a的值;
(3)不等式|
| f(x)+a[g(x)-2a] |
| f(x) |
|
解答: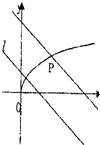 解:(1)∵F(x)=f(x)+g(x)=-x+
解:(1)∵F(x)=f(x)+g(x)=-x+
+a=-(
-
)2+a+
,
易得当
≥
,即x∈[
,+∞)时,F(x)单调递减
即函数的单调递减区间是[
,+∞)
(2)G(x)=
,其图象如图,
由图象得,所求的最小值即为点P到直线的距离,亦即两平行线x+y-1=0与x+y-a=0之间的距离
由
=
,且a>1,得a=3
(3)由|
|≤1得|
| =|1-a(
+
)|≤1
即-1≤1-a(
+
)≤1
即0≤a(
+
)≤2对x∈[1,4]恒成立
当x=1,x=4分别代入得
解得0<a≤2
-2
 解:(1)∵F(x)=f(x)+g(x)=-x+
解:(1)∵F(x)=f(x)+g(x)=-x+| x |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
易得当
| x |
| 1 |
| 2 |
| 1 |
| 4 |
即函数的单调递减区间是[
| 1 |
| 4 |
(2)G(x)=
|
由图象得,所求的最小值即为点P到直线的距离,亦即两平行线x+y-1=0与x+y-a=0之间的距离
由
| |a-1| | ||
|
| 2 |
(3)由|
| f(x)+a[g(x)-2a] |
| f(x) |
| ||
|
| x |
| a | ||
|
即-1≤1-a(
| x? |
| a | ||
|
即0≤a(
| x? |
| a | ||
|
当x=1,x=4分别代入得
|
| 2 |
点评:本题考查函数最值的应用,解题的关键是判断出函数最值的位置及利用函数的最值建立方程求参数,函数最值是函数一个重要的性质,其题型一般有判断最值求最值,及利用最值建立方程求参数,函数最值考查的题型也是高考中的觉题型,要注意积累函数最值的判断方法及函数最值的用法,本题综合性强,较抽象,解题时转化要严谨,运算认真

练习册系列答案
相关题目