题目内容
等比数列{an}的前n项和为Sn, 已知对任意的n∈N*,点(n,Sn),均在函数y=bx+r(b>0且b≠1,b,r均为常数)的图像上。
(1)求r的值;
(2)当b=2时,记 bn=2(log2an+1)(n∈N*)用数学归纳法证明:对任意的n∈N*,不等式 成立。
成立。
(1)求r的值;
(2)当b=2时,记 bn=2(log2an+1)(n∈N*)用数学归纳法证明:对任意的n∈N*,不等式
 成立。
成立。解:(1)因为对任意的n∈N*,点(n,Sn),均在函数y=bx+r(b>0且b≠1,b,r均为常数)的图像上。
所以得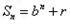 ,
,
当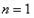 时,
时, ;
;
当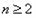 时,
时,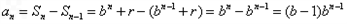
又因为{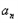 }为等比数列
}为等比数列
所以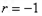 ,公比为b,
,公比为b,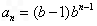
(2)当b=2时,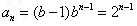 ,
,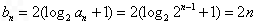
则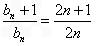 ,所以
,所以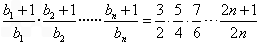
下面用数学归纳法证不等式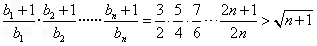 成立。
成立。
当n=1时,左边=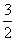 ,右边=
,右边=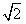 ,因为
,因为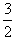 >
>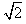 ,所以不等式成立
,所以不等式成立
② 假设当n=k 时,不等式成立,即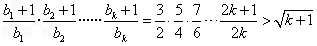 成立
成立
则当n=k+1时,左边=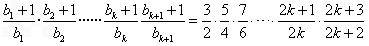
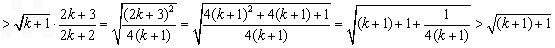
所以当n=k+1时,不等式成立。
由①、②可得不等式恒成立。
所以得
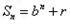 ,
,当
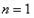 时,
时, ;
;当
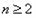 时,
时,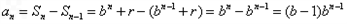
又因为{
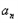 }为等比数列
}为等比数列所以
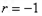 ,公比为b,
,公比为b,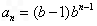
(2)当b=2时,
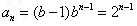 ,
,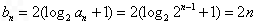
则
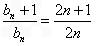 ,所以
,所以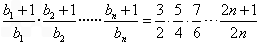
下面用数学归纳法证不等式
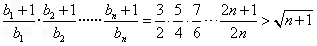 成立。
成立。当n=1时,左边=
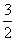 ,右边=
,右边=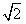 ,因为
,因为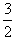 >
>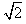 ,所以不等式成立
,所以不等式成立② 假设当n=k 时,不等式成立,即
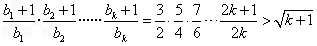 成立
成立则当n=k+1时,左边=
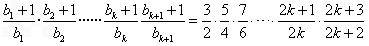
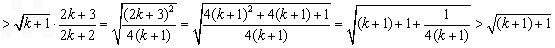
所以当n=k+1时,不等式成立。
由①、②可得不等式恒成立。

练习册系列答案
相关题目
 (2012•蓝山县模拟)统计某校高三年级100名学生的数学月考成绩,得到样本频率分布直方图如下图所示,已知前4组的频数分别是等比数列{an}的前4项,后6组的频数分别是等差数列{bn}的前6项,
(2012•蓝山县模拟)统计某校高三年级100名学生的数学月考成绩,得到样本频率分布直方图如下图所示,已知前4组的频数分别是等比数列{an}的前4项,后6组的频数分别是等差数列{bn}的前6项,