题目内容
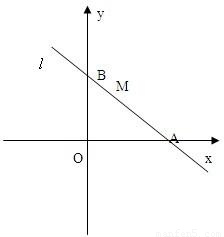
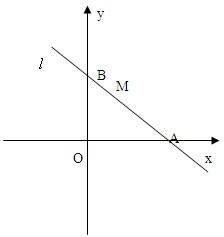 已知直线l过点M(1,2),且直线l与x轴正半轴和y轴的正半轴交点分别是A、B,(如图,注意直线l与坐标轴的交点都在正半轴上)
已知直线l过点M(1,2),且直线l与x轴正半轴和y轴的正半轴交点分别是A、B,(如图,注意直线l与坐标轴的交点都在正半轴上)(1)若三角形AOB的面积是4,求直线l的方程.
(2)求过点N(0,1)且与直线m垂直的直线方程.
分析:(1)要求直线l方程,因为点已知,所以要求出直线l的斜率.可设出斜率为k,写出直线l方程,分别求出与x轴、y轴的截距表示出三角形AOB的面积等于4,列出方程即可求出k;
(2)因为直线m与直线l垂直,根据直线l的斜率求出直线m的斜率,即可得到直线m的方程.
(2)因为直线m与直线l垂直,根据直线l的斜率求出直线m的斜率,即可得到直线m的方程.
解答:解:(1)设直线l的斜率是k,直线l的方程y-2=k(x-1)
当x=0时,y=2-k即OB=2-k当y=0时,x=1-
即OA=1-
所以三角形AOB分面积是
×OA×OB=
×(2-k)(1-
)=4
整理得:k2+4k+4=0解得k=-2所以直线方程是y-2=-2(x-1)
即y=-2x+4;
(2)由(1)知,直线l的斜率为-2,因为直线m与直线l垂直即斜率乘积为-1可得直线m的斜率是
则直线方程是:y-1=
(x-0),即y=
x+1.
当x=0时,y=2-k即OB=2-k当y=0时,x=1-
| 2 |
| k |
| 2 |
| k |
所以三角形AOB分面积是
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| k |
整理得:k2+4k+4=0解得k=-2所以直线方程是y-2=-2(x-1)
即y=-2x+4;
(2)由(1)知,直线l的斜率为-2,因为直线m与直线l垂直即斜率乘积为-1可得直线m的斜率是
| 1 |
| 2 |
则直线方程是:y-1=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题为一道综合题,要求学生会根据直线与坐标轴截取的三角形面积求出直线的斜率,掌握两直线垂直时斜率乘积为-1,会根据直线斜率和一点坐标写出直线的一般式方程.

练习册系列答案
相关题目
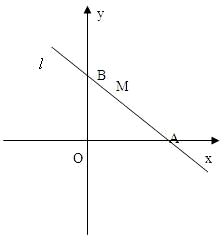 已知直线l过点M(1,2),且直线l与x轴正半轴和y轴的正半轴交点分别是A、B,(如图,注意直线l与坐标轴的交点都在正半轴上)
已知直线l过点M(1,2),且直线l与x轴正半轴和y轴的正半轴交点分别是A、B,(如图,注意直线l与坐标轴的交点都在正半轴上)