题目内容
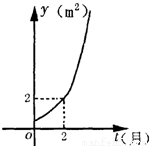
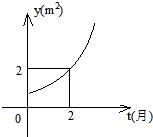 某池塘中原有一块浮草,浮草蔓延后的面积y(m2)与时间t(月)之间的函数关系是y=at-1(a>0且a≠1),它的图象如图所示:
某池塘中原有一块浮草,浮草蔓延后的面积y(m2)与时间t(月)之间的函数关系是y=at-1(a>0且a≠1),它的图象如图所示:
①池塘中原有浮草的面积是0.5m2;
②到第7个月浮草的面积一定能超过60m2;
③浮草每月增加的面积都相等;
④若浮草面积达到4m2,16m2,64m2所经过的时间分别为t1,t2,t3,则t1+t2<t3.
其中所有正确命题的序号为 ________.
①②
分析:先根据图象经过点(2,2)求出a,然后对没有个选支进行逐一判断即可.
解答:根据图象过点(2,2)可知
点(2,2)适合y=at-1即2=a
∴函数关系是y=2t-1
令t=0时,y= =0.5,故①正确
=0.5,故①正确
令t=7时,y=26=64>60,故②正确
当t=1时,y=1,增加0.5,当t=2时,y=2,增加1,每月增加的面积不相等,故③不正确
分别令y=4、16、64,解得t1=3,t2=5,t3=7,t1+t2>t3,故④不正确
故答案为:①②
点评:本题主要考查了指数函数的图象与性质,以及求函数值等有关基础知识,同时考查识图能力,数形结合的思想,属于基础题.
分析:先根据图象经过点(2,2)求出a,然后对没有个选支进行逐一判断即可.
解答:根据图象过点(2,2)可知
点(2,2)适合y=at-1即2=a
∴函数关系是y=2t-1
令t=0时,y=
 =0.5,故①正确
=0.5,故①正确令t=7时,y=26=64>60,故②正确
当t=1时,y=1,增加0.5,当t=2时,y=2,增加1,每月增加的面积不相等,故③不正确
分别令y=4、16、64,解得t1=3,t2=5,t3=7,t1+t2>t3,故④不正确
故答案为:①②
点评:本题主要考查了指数函数的图象与性质,以及求函数值等有关基础知识,同时考查识图能力,数形结合的思想,属于基础题.

练习册系列答案
相关题目
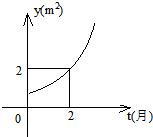 某池塘中原有一块浮草,浮草蔓延后的面积y(m2)与时间t(月)之间的函数关系是y=at-1(a>0且a≠1),它的图象如图所示:
某池塘中原有一块浮草,浮草蔓延后的面积y(m2)与时间t(月)之间的函数关系是y=at-1(a>0且a≠1),它的图象如图所示: 某池塘中原有一块浮草,浮草蔓延后的面积y(m2)与时间t(月)之间的函数关系是y=at-1(a>0,且a≠1),它的图象如图所示.给出以下命题:
某池塘中原有一块浮草,浮草蔓延后的面积y(m2)与时间t(月)之间的函数关系是y=at-1(a>0,且a≠1),它的图象如图所示.给出以下命题: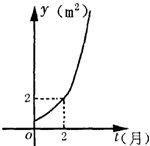 某池塘中原有一块浮草,浮草蔓延后的面积y(m2)与时间t(月)之间的函数关系是y=at-1(a>0,且a≠1),它的图象如图所示.给出以下命题:
某池塘中原有一块浮草,浮草蔓延后的面积y(m2)与时间t(月)之间的函数关系是y=at-1(a>0,且a≠1),它的图象如图所示.给出以下命题: