题目内容
(本题满分14分) 甲、乙两队各有n个队员，已知甲队的每个队员分别
与乙队的每个队员各握手一次 (同队的队员之间不握手)，从这n2次的握手中任意取两次．记
事件A：两次握手中恰有4个队员参与；
事件B：两次握手中恰有3个队员参与．
(Ⅰ) 当n＝4时，求事件A发生的概率P(A)；
(Ⅱ) 若事件B发生的概率P (B)＜
，求n的最小值．
与乙队的每个队员各握手一次 (同队的队员之间不握手)，从这n2次的握手中任意取两次．记事件A：两次握手中恰有4个队员参与；
事件B：两次握手中恰有3个队员参与．
(Ⅰ) 当n＝4时，求事件A发生的概率P(A)；
(Ⅱ) 若事件B发生的概率P (B)＜
，求n的最小值．(Ⅰ)
(Ⅱ)n的最小值为20
(Ⅰ) 解：样本空间包含的基本事件总数为C
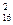，事
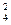件A包含的基本事件总数为2C
C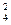，所以P(A)＝
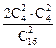＝． …………………7分(Ⅱ) 因为样本空间包含的基本事件总数为C
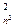，事件B包含的基本事件总数为2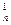C
C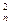
，所以P(B)＝
＝
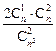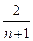＜，故n＞19，即n≥20．
而当n＝20时，P(B)=
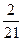＜，综上， n的最小值为20．…………………………14分
练习册系列答案
相关题目
，画出如下图所示的部分频率分布直方图，请观察图形信息，回答下列问题：
的概率分布列及数学期望。
和
，则（ ）
=