Question

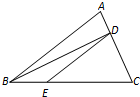已知△ABC的面积为1，点D在AC上，DE∥AB，连接BD，设△DCE、△ABD、△BDE中面积最大者的值为y，则y的最小值为

3- 5

2

．

Answer 1

分析：先分别求出△DCE、△ABD、△BDE中面积，确定最大值，可得分段函数，即可求得y的最小值．

解答：解：设CD：CA=k，则因为点D在AC上，所以0＜k＜1
∵DE∥AB，∴△DCE∽△ACB，∴S_△DCE：S_△ACB=（CD：CA）²=k²，
∵S_△ABC=1，∴S_△DCE=k²；
∵AD：AC=（AC-CD）：AC=1-k，∴S_△ABD：S_△ABC=AD：AC=1-k，∴S_△ABD=1-k
∵DE∥AB，∴CE：BE=CD：AD=k：（1-k）
∵S_△DCE：S_△BDE=CE：BE=k：（1-k）
∴S_△BDE=[（1-k）：k]×S_△DCE=-k²+k
当k²=1-k时，k²+k-1=0，∴k=

-1+ 5

2

；当k²=-k²+k时，2k²-k=0，∴k=

1

2

；
当1-k=-k²+k时，k²-2k+1=0，∴k=1
∴y=

1-k，0＜k≤ -1+ 5 2 k2， -1+ 5 2 ＜k＜1

∴当k=

-1+ 5

2

时，y有最小值=1-k=k²=

3- 5

2

故答案为：

3- 5

2

点评：本题考查三角形面积的计算，考查函数的最值，考查分段函数，考查学生分析解决问题的能力，属于中档题．