题目内容
已知l1是过原点O,且与向量
=(2,-λ)垂直的直线,l2是过定点A(0,2),且与向量
=(-1,
)平行的直线,则l1与l2交点P的轨迹方程是
| a |
| b |
| λ |
| 2 |
x2+(y-1)2=1
x2+(y-1)2=1
,轨迹是以(0,1)为圆心,1为半径的圆
以(0,1)为圆心,1为半径的圆
.分析:先根据条件分别写出两直线的方程,再联立消去参数,就可得到P点的轨迹方程,从而得出答案.
解答:解:∵l1是过原点O,且与向量
=(2,-λ)垂直的直线,
∴直线l1的方程为y=
x,①
∵l2是过定点A(0,2),且与向量
=(-1,
)平行的直线,
∴直线l2的方程为y-2=-
x,②
∴①×②得y(y-2)=-x2
化简得x2+(y-1)2=1.
故答案为:x2+(y-1)2=1,以(0,1)为圆心,1为半径的圆
| a |
∴直线l1的方程为y=
| 2 |
| λ |
∵l2是过定点A(0,2),且与向量
| b |
| λ |
| 2 |
∴直线l2的方程为y-2=-
| λ |
| 2 |
∴①×②得y(y-2)=-x2
化简得x2+(y-1)2=1.
故答案为:x2+(y-1)2=1,以(0,1)为圆心,1为半径的圆
点评:本题考查了向量在几何中的应用,参数法求点的轨迹方程,恰当的引入参数,并能巧妙地消去参数得轨迹方程是解决本题的关键

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
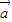 =(2,-λ)垂直的直线,l2是过定点A(0,2),且与向量
=(2,-λ)垂直的直线,l2是过定点A(0,2),且与向量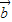 =
=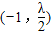 平行的直线,则l1与l2交点P的轨迹方程是 ,轨迹是 .
平行的直线,则l1与l2交点P的轨迹方程是 ,轨迹是 .