题目内容
设n∈N,若(1+x)n=a0+a1x+a2x2+…+anxn,且a1+a2=21,则在(1+x)n 的展开式的各项系数中,最大系数的值是
35
35
.分析:求出展开式的含x,x2的系数,列出方程,求出n值;据二项式系数的性质中间项的二项式系数最大求出展开式的各项系数中最大系数的值.
解答:解:∵a1,a2分别是(1+x)n展开式中含x及x2项的系数
∴a1=Cn1 a2=Cn2
∴Cn1+Cn2=21
解得n=6
所以(1+x)n展开式中共7项,且展开式项的系数与二项式系数相同
故展开式中第四项的系数最大,最大为C73=35
故答案为:35
∴a1=Cn1 a2=Cn2
∴Cn1+Cn2=21
解得n=6
所以(1+x)n展开式中共7项,且展开式项的系数与二项式系数相同
故展开式中第四项的系数最大,最大为C73=35
故答案为:35
点评:求二项展开式中的特殊项问题,常利用二项展开式的通项公式.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
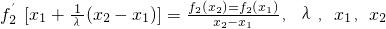 为常数.
为常数.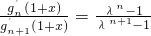 在区间(0,2)上有唯一实数根;记此实数根为x(n),求x(n)的最大值.
在区间(0,2)上有唯一实数根;记此实数根为x(n),求x(n)的最大值.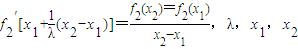 为常数.
为常数.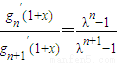 在区间(0,2)上有唯一实数根;记此实数根为x(n),求x(n)的最大值.
在区间(0,2)上有唯一实数根;记此实数根为x(n),求x(n)的最大值.