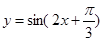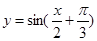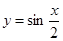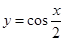题目内容
已知方程 在
在 上有两个不同的解
上有两个不同的解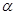 、
、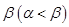 ,则下列结论正确的是( )
,则下列结论正确的是( )
A.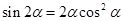 | B.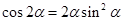 |
C. | D. |
C
解析试题分析:由于方程 在
在 上有两个不同的解
上有两个不同的解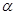 、
、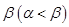 ,即方程
,即方程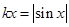 在
在 上有两个不同的解
上有两个不同的解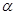 、
、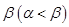 ,也就是说,直线
,也就是说,直线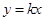 与函数
与函数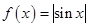 在
在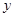 轴右侧的图象有且仅有两个交点,由图象可知,当
轴右侧的图象有且仅有两个交点,由图象可知,当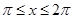 时,直线
时,直线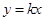 与曲线
与曲线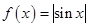 相切,且切点的横坐标为
相切,且切点的横坐标为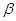 ,
,
当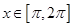 时,
时,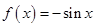 ,则
,则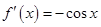 ,故
,故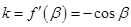 ,在切点处有
,在切点处有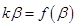
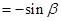 ,即
,即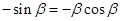 ,
,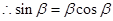 ,两边同时乘以
,两边同时乘以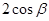 得,
得, ,故选C.
,故选C.
考点:1.函数的零点;2.函数的图象;3.利用导数求切线的斜率

练习册系列答案
相关题目
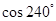 的值是( )
的值是( )
A. | B.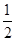 | C.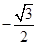 | D. |
已知函数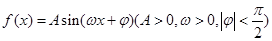 的部分图像如图所示,则
的部分图像如图所示,则 的图像可由函数
的图像可由函数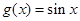 的图像(纵坐标不变)( )
的图像(纵坐标不变)( )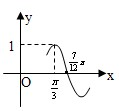
A.先把各点的横坐标缩短到原来的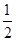 倍,再向右平移 倍,再向右平移 个单位 个单位 |
B.先把各点的横坐标伸长到原来的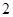 倍,再向右平移 倍,再向右平移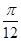 个单位 个单位 |
C.先向右平移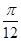 个单位,再把各点的横坐标伸长到原来的 个单位,再把各点的横坐标伸长到原来的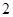 倍 倍 |
D.先向右平移 个单位,再把各点的横坐标缩短到原来的 个单位,再把各点的横坐标缩短到原来的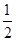 倍 倍 |
函数 的图象如图所示,则函数的表达式为( )
的图象如图所示,则函数的表达式为( )
A. | B. |
C. | D. |
若 ,则
,则 的值为( )
的值为( )
A. | B.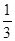 | C. | D. |
已知 ,则函数
,则函数 的最大值是( )
的最大值是( )
| A.3 | B. | C. | D. |
若 且
且 ,则
,则 ( )
( )
A. | B. | C. | D. |
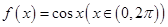 有两个不同的零点
有两个不同的零点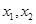 ,方程
,方程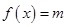 有两个不同的实根
有两个不同的实根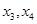 .若这四个数按从小到大排列构成等差数列,则实数
.若这四个数按从小到大排列构成等差数列,则实数 的值为( )
的值为( )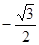


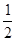
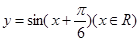 图像上所有的点向左平行移动
图像上所有的点向左平行移动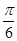 个单位长度,再把图像上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得到的图像的解析式为( )
个单位长度,再把图像上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得到的图像的解析式为( )