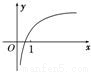题目内容
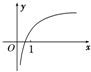 设m,n∈R,函数y=m+lognx的图象如图所示,则有
设m,n∈R,函数y=m+lognx的图象如图所示,则有
- A.m<0,0<n<1
- B.m>0,n>1
- C.m>0,0<n<1
- D.m<0,n>1
B
分析:由函数图象知是增函数,则n>1,又因图象与x轴的交点在(0,1)之间和上下平移法则得m>0.
解答:由函数图象可知该函数为增函数,所以n>1,
因图象与x轴的交点在(0,1)之间,故该图象是由y=lognx的图象向上平移得到的,所以m>0.
故选B.
点评:本题考查了对数函数的图象和图象的上下平移法则,考查了读图能力.
分析:由函数图象知是增函数,则n>1,又因图象与x轴的交点在(0,1)之间和上下平移法则得m>0.
解答:由函数图象可知该函数为增函数,所以n>1,
因图象与x轴的交点在(0,1)之间,故该图象是由y=lognx的图象向上平移得到的,所以m>0.
故选B.
点评:本题考查了对数函数的图象和图象的上下平移法则,考查了读图能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
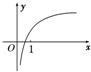 3、设m,n∈R,函数y=m+lognx的图象如图所示,则有( )
3、设m,n∈R,函数y=m+lognx的图象如图所示,则有( )