题目内容
已知函数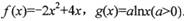
(I)若直线l1交函数f(x)的图象于P,Q两点,与l1平行的直线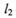 与函数
与函数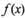 的图象切于点R,求证 P,R,Q三点的横坐标成等差数列;
的图象切于点R,求证 P,R,Q三点的横坐标成等差数列;
(II)若不等式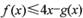 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(III)求证: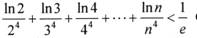 〔其中
〔其中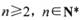 , e为自然对数的底数)
, e为自然对数的底数)
【答案】
(Ⅰ)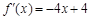 ,设切点R(x0,y0)
,设切点R(x0,y0)
则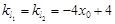 .
.
令l2:y=(-4x0+4)x+b.
联立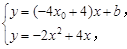 消去y得 2x2-4x0x+b=0.
消去y得 2x2-4x0x+b=0.
令P(x1,y1),Q(x2,y2),则x1+x2=2x0,
即R、R、Q三点的横坐标成等差数列. ……………………………………4分
(Ⅱ)由已知有f (x)+g(x)-4x=-2x2+alnx≤0恒成立,
令F(x)=2x2-alnx(x>0),
则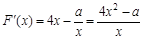 .
.
由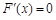 ,得
,得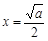 .
.
当0<x<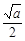 时
时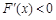 ,F(x)在区间(0,
,F(x)在区间(0,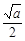 )上递减;
)上递减;
当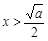 时,
时,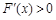 ,F(x)在区间(
,F(x)在区间(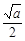 ,+∞)上递增.
,+∞)上递增.
∴ 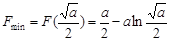 ≥0,得0<a≤4e.……………………………9分
≥0,得0<a≤4e.……………………………9分
(Ⅲ)由(2)知当a=2e时有2x2-2elnx≥0,得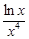 ≤
≤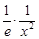
∴ 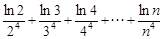
≤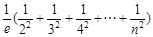
<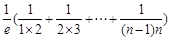
=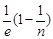
<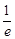 .
.
【解析】略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 函数
函数 .
. 且函数
且函数 为奇函数,求实数
为奇函数,求实数 ;
; 试判断函数
试判断函数 ,
, ,
, 时,求函数
时,求函数 的对称轴或对称中心.
的对称轴或对称中心.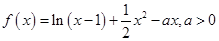 .
.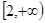 的最小值为f(t),求t的值。
的最小值为f(t),求t的值。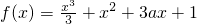 ,动直线l的斜率k=2.
,动直线l的斜率k=2.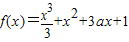 ,动直线l的斜率k=2.
,动直线l的斜率k=2.