题目内容
已知an=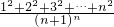 n∈N*求证:an<1.
n∈N*求证:an<1.
证明:(1)当n=1时,a1= <1,不等式成立.
<1,不等式成立.
(2)假设n=k(k≥1)时,不等式成立,即ak=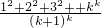 <1
<1
亦即1+22+32+…+k2<(k+1)k
当n=k+1时:ak+1=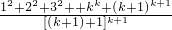 <
<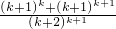 =
=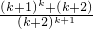 =(
=(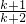 )k<1.
)k<1.
所以n=k+1时,不等式也成立.
由(1)、(2)知,对一切n∈N*,不等式都成立.
即an<1得证.
分析:首先分析题目已知an=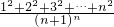 求证:an<1.考虑到可以应用数学归纳法求解,首先验证当n=1时,不等式成立,再假设n=k(k≥1)时,不等式成立,推得当n=k+1时不等式也成立.即得证.
求证:an<1.考虑到可以应用数学归纳法求解,首先验证当n=1时,不等式成立,再假设n=k(k≥1)时,不等式成立,推得当n=k+1时不等式也成立.即得证.
点评:此题主要考查由数学归纳法证明不等式,数学归纳法在高考中属于重要的考点,应用广泛,需要同学们灵活掌握.
 <1,不等式成立.
<1,不等式成立.(2)假设n=k(k≥1)时,不等式成立,即ak=
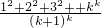 <1
<1亦即1+22+32+…+k2<(k+1)k
当n=k+1时:ak+1=
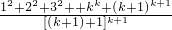 <
<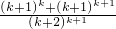 =
=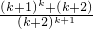 =(
=(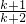 )k<1.
)k<1.所以n=k+1时,不等式也成立.
由(1)、(2)知,对一切n∈N*,不等式都成立.
即an<1得证.
分析:首先分析题目已知an=
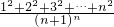 求证:an<1.考虑到可以应用数学归纳法求解,首先验证当n=1时,不等式成立,再假设n=k(k≥1)时,不等式成立,推得当n=k+1时不等式也成立.即得证.
求证:an<1.考虑到可以应用数学归纳法求解,首先验证当n=1时,不等式成立,再假设n=k(k≥1)时,不等式成立,推得当n=k+1时不等式也成立.即得证.点评:此题主要考查由数学归纳法证明不等式,数学归纳法在高考中属于重要的考点,应用广泛,需要同学们灵活掌握.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目

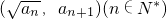 在函数y=x2+1的图象上.数列{bn}满足b1=0,bn+1=bn+3an(n∈N*).
在函数y=x2+1的图象上.数列{bn}满足b1=0,bn+1=bn+3an(n∈N*).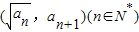 在函数y=x2+1的图象上.数列{bn}满足b1=0,bn+1=bn+3an(n∈N*).
在函数y=x2+1的图象上.数列{bn}满足b1=0,bn+1=bn+3an(n∈N*).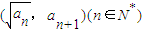 在函数y=x2+1的图象上.数列{bn}满足b1=0,bn+1=bn+3an(n∈N*).
在函数y=x2+1的图象上.数列{bn}满足b1=0,bn+1=bn+3an(n∈N*).