题目内容
下列曲线的所有切线构成的集合中,切线斜率恒大于零的曲线是
- A.y=sinx
- B.y=cosx
- C.y=x2
- D.y=ex
D
分析:求出四个选项对应的函数的导数,判断函数的导数的值域范围,即可得到结果.
解答:因为y=sinx的导数为y′=cosx∈[-1,1];切线斜率不恒大于零,A不正确;
因为y=cosx的导数为y′=-sinx∈[-1,1];切线斜率不恒大于零,B不正确;
因为y=x2的导数为y′=2x∈R,切线斜率不恒大于零,C不正确;
因为y=xe的导数为y′=xe>0,切线斜率恒大于零,D正确;
故选D.
点评:本题考查导数的几何意义、导函数的值域与切线的斜率的关系,考查计算能力.
分析:求出四个选项对应的函数的导数,判断函数的导数的值域范围,即可得到结果.
解答:因为y=sinx的导数为y′=cosx∈[-1,1];切线斜率不恒大于零,A不正确;
因为y=cosx的导数为y′=-sinx∈[-1,1];切线斜率不恒大于零,B不正确;
因为y=x2的导数为y′=2x∈R,切线斜率不恒大于零,C不正确;
因为y=xe的导数为y′=xe>0,切线斜率恒大于零,D正确;
故选D.
点评:本题考查导数的几何意义、导函数的值域与切线的斜率的关系,考查计算能力.

练习册系列答案
相关题目
下列曲线的所有切线构成的集合中,存在无数对互相垂直的切线的曲线是( )
| A、f(x)=ex | B、f(x)=x3 | C、f(x)=lnx | D、f(x)=sinx |
 ②
② ③
③ ④
④
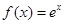 ②
② ③
③ ④
④