题目内容
设函数y=f（x）sinx的图象为C1，将C1向右平移
个单位，可得曲线C2，若曲线C2与函数y=cos2x的图象关于x轴对称，那么f（x）可以是________．
f（x）=2cosx
分析：由题意曲线C2与函数y=cos2x的图象关于x轴对称，先求曲线C2的方程，再用函数y=f（x）sinx的图象为C1，将C1向右平移个单位，可得曲线C2，求出C2的方程，两者相同，化简可求f（x）
解答：曲线C2与函数y=cos2x的图象关于x轴对称，所以曲线C2的方程为：y=-cos2x；
函数y=f（x）sinx的图象为C1，将C1向右平移个单位，可得曲线C2，
所以C2的方程又可以表示为：y=f（x
）sin（x）
所以 f（x）sin（x）=-cos2x
化简得f（x）=2sin（x+）
所以：f（x）=2cosx
故答案为：f（x）=2cosx
点评：本题考查函数y=Asin（ωx+φ）的图象变换，二倍角的余弦，两角和与差的三角函数，考查学生计算能力，是中档题．
分析：由题意曲线C2与函数y=cos2x的图象关于x轴对称，先求曲线C2的方程，再用函数y=f（x）sinx的图象为C1，将C1向右平移
个单位，可得曲线C2，求出C2的方程，两者相同，化简可求f（x）解答：曲线C2与函数y=cos2x的图象关于x轴对称，所以曲线C2的方程为：y=-cos2x；
函数y=f（x）sinx的图象为C1，将C1向右平移
个单位，可得曲线C2，所以C2的方程又可以表示为：y=f（x
）sin（x）所以 f（x
）sin（x）=-cos2x化简得f（x
）=2sin（x+）所以：f（x）=2cosx
故答案为：f（x）=2cosx
点评：本题考查函数y=Asin（ωx+φ）的图象变换，二倍角的余弦，两角和与差的三角函数，考查学生计算能力，是中档题．
练习册系列答案
阅读快车系列答案
相关题目
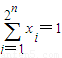，证明：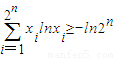
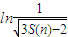（i，n∈N*）．