函数f(x)=$\frac{1}{2}$x-sinx的图象是( )A．B．C．D．题目和参考答案——青夏教育精英家教网——

题目内容

9．函数f（x）=$\frac{1}{2}$x-sinx的图象是（　　）

A．

B．

C．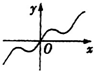

D．

分析先根据函数的奇偶性排除B，D，再根据特殊值排除C，问题得以解决．

解答解：∵f（-x）=-$\frac{1}{2}$x+sinx=-（$\frac{1}{2}$x-sinx）=-f（x），
∴f（x）为奇函数，即图象关于原点对称，排除B，D，
当x=$\frac{π}{2}$时，f（$\frac{π}{2}$）=$\frac{π}{4}$-1＜0，故排除C，
故选：A

点评本题考查了函数图象的识别，关键求出函数的奇偶性，以及利用特殊值，属于基础题．

练习册系列答案

单元测试四川教育出版社系列答案

少年素质教育报综合检测系列答案

清华绿卡期末卷系列答案

课后练习专题精析系列答案

双测AB卷系列答案

新思维成才典对典系列答案

各地初中期末汇编系列答案

单元双测全优测评卷系列答案

师大测评卷期末点津系列答案

课堂同步提优系列答案

相关题目

19．已知函数f（x）=lnx+x²-2ax+1（a为常数）．
（Ⅰ）讨论函数f（x）的单调性；
（Ⅱ）证明：若对任意的a∈（1，$\sqrt{2}$），都存在x₀∈（0，1]使得不等式f（x₀）+lna＞a-a²成立．

20．已知点（a_n，n）在函数y=log₂x的图象上，则符合数列{a_n}的一个递推公式为（　　）

	A．	a₁=1，a_n+1=a_n+2^n-1		B．	a₁=1，a_n+1=a_n+2ⁿ
	C．	a₁=2，a_n+1=a_n+2^n-1		D．	a₁=2，a_n+1=4a_n-2ⁿ⁺¹

17．有以下四种变换方式：
①向左平移$\frac{π}{4}$个单位长度，再将每个点的横坐标缩短为原来的$\frac{1}{2}$倍；
②向右平移$\frac{π}{8}$个单位长度，再将每个点的横坐标缩短为原来的$\frac{1}{2}$倍；
③每个点的横坐标缩短为原来的$\frac{1}{2}$倍，再向右平移$\frac{π}{8}$个单位长度；
④每个点的横坐标缩短为原来的$\frac{1}{2}$倍，再向左平移$\frac{π}{8}$个单位长度．
其中能将y=2sinx的图象变为$y=2sin（2x+\frac{π}{4}）$的图象的是（　　）

4．已知圆M：（x+cosθ）²+（y-sinθ）²=1，直线l：y=kx，以下结论成立的有②⑤．（写出所有正确结论的编号）
①对任意实数k与θ，直线l和圆M相切；②对任意实数k与θ，直线l和圆M有公共点；
③存在实数k与θ，直线l和圆M相离； ④对任意实数θ，必存在实数k，使得直线l和圆M相切；
⑤对任意实数k，必存在实数θ，使得直线l和圆M相切．

14．在△ABC中，角A，B，C的对边分别是a，b，c，且$\sqrt{3}$acosC=（2b-$\sqrt{3}$c）cosA．
（1）求角A的大小；
（2）求cos（$\frac{5π}{2}$-B）-2sin²$\frac{C}{2}$的取值范围．

1．已知函数f（x）=1+x-$\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+…-\frac{{{x^{2014}}}}{2014}+\frac{{{x^{2015}}}}{2015}$，若函数f（x）的零点都在[a，b]（a＜b，a，b∈Z）内，则b-a的最小值是1．

18．设A为非空实数集，若?x，y∈A都有x+y，x-y，xy∈A，则称A为封闭集．
①集合A={-2，-1，0，1，1}为封闭集；②集合A={n|n=2k，k∈Z}为封闭集；
③若集合A₁，A₂为封闭集，则A₁∪A₂为封闭集；
④若A为封闭集，则一定有0∈A．
其中正确结论的序号是②④．

19．设坐标原点为O，已知过点（0，$\frac{1}{2}$）的直线交函数y=$\frac{1}{2}$x²的图象于A、B两点，则$\overrightarrow{OA}$•$\overrightarrow{OB}$的值为（　　）