题目内容
设点P(x,y)(y≥0)为平面直角坐标系xOy中的一个动点(其中O为坐标原点),点P到定点M(0, )的距离比点P到x轴的距离大
)的距离比点P到x轴的距离大 .
.(1)求点P的轨迹方程;
(2)若直线l:y=x+1与点P的轨迹相交于A、B两点,求线段AB的长;
(3)设点P的轨迹是曲线C,点Q(1,y)是曲线C上一点,求过点Q的曲线C的切线方程.
【答案】分析:(1)用直接法或定义法求得点P轨迹方程.
(2)联立y=x+1与x2=2y化简得x2-2x-2=0,把根与系数的关系代入弦长公式求出结果.
(3)曲线C即函数y=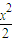 的图象,利用导数求得切线的斜率,点斜式求得切线的方程.
的图象,利用导数求得切线的斜率,点斜式求得切线的方程.
解答:解:(1)用直接法或定义法求得点P轨迹方程为x2=2y.
(2)联立y=x+1与x2=2y化简得x2-2x-2=0. 设A(x1,y1),B(x2,y2),则x1+x2=2,x1x2=-2,
|AB|=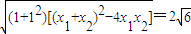 .
.
(3)曲线C即函数y=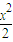 的图象,y′=x,y′|x=1=1,又Q(1,
的图象,y′=x,y′|x=1=1,又Q(1, ),
),
故所求切线方程为y- =1•(x-1)即x-y-
=1•(x-1)即x-y- =0.
=0.
点评:本题考查抛物线的定义、标准方程,以及简单性质的应用,求出切线的斜率是解题的关键.
(2)联立y=x+1与x2=2y化简得x2-2x-2=0,把根与系数的关系代入弦长公式求出结果.
(3)曲线C即函数y=
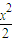 的图象,利用导数求得切线的斜率,点斜式求得切线的方程.
的图象,利用导数求得切线的斜率,点斜式求得切线的方程.解答:解:(1)用直接法或定义法求得点P轨迹方程为x2=2y.
(2)联立y=x+1与x2=2y化简得x2-2x-2=0. 设A(x1,y1),B(x2,y2),则x1+x2=2,x1x2=-2,
|AB|=
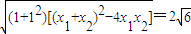 .
.(3)曲线C即函数y=
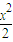 的图象,y′=x,y′|x=1=1,又Q(1,
的图象,y′=x,y′|x=1=1,又Q(1, ),
),故所求切线方程为y-
 =1•(x-1)即x-y-
=1•(x-1)即x-y- =0.
=0.点评:本题考查抛物线的定义、标准方程,以及简单性质的应用,求出切线的斜率是解题的关键.

练习册系列答案
相关题目