题目内容
（本题满分12分）某校从高一年级学生中随机抽取40名学生，将他们的期中考试数学成绩（满分100分，成绩均为不低于40分的整数）分成六段：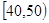
，
，…，
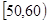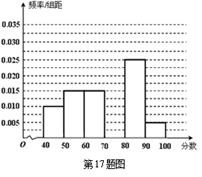
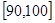后得到如图的频率分布直方图．
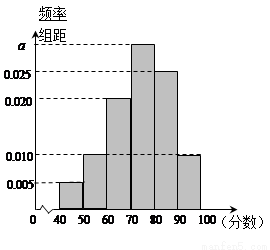
（1）求图中实数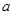
的值；
（2）若该校高一年级共有学生640人，试估计该校高一年级
期中考试数学成绩不低于60分的人数；
（3）若从数学成绩在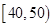
与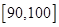
两个分数段内的学生中随机选取两名学生，求这两名学生的数学成绩之差的绝对值不大于10的概率．
（1）
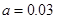（2）544（3）
【解析】
试题分析：（1）由于图中所有小矩形的面积之和等于1，
所以
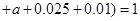． ……2分
解得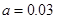． ……3分
（2）根据频率分布直方图，成绩不低于60分的频率
为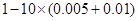
． ……5分
由于该校高一年级共有学生640人，利用样本估计总体的思想，
可估计该校高一年级数学成绩不低于60分的人数约为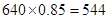
人． ……6分
（3）成绩在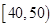
分数段内的人数为
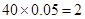人，分别记为
，
． ……7分
成绩在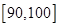
分数段内的人数为
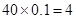人，分别记为
，
，
，
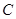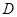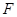． ……8分
若从数学成绩在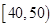与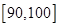两个分数段内的学生中随机选取两名学生，
则所有的基本事件有：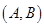
，
，
，
，
，
，
，
，
，
，
，
，
，
，
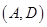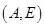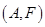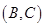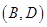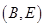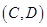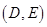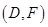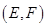共15种． ……10分
如果两名学生的数学成绩都在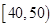分数段内或都在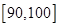分数段内，那么这两名学生的数学成绩之差的绝对值一定不大于10.如果一个成绩在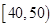分数段内，另一个成绩在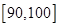分数段内，那么这两名学生的数学成绩之差的绝对值一定大于10．
记“这两名学生的数学成绩之差的绝对值不大于10”为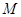事件
，则事件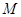包含的基本事件有：
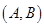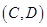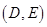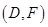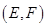，，，，，，共7种． ……11分
所以所求概率为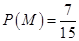
． ……12分
考点：本小题主要考查频率分布直方图的应用和古典概型概率的求解，考查学生识图、用图的能力和运算求解能力.
点评：解决与频率分布直方图有关的题目时，要注意到频率分布直方图中纵轴表示的是
频率/组距，不是频率，图中小矩形的面积才表示频率.
名学生，将其数学成绩（均为整数）分成六段
，
…
后得到如下部分频率分布直方图.观察图形的信息，回答下列问题：
内的频率，并补全这个频率分布直方图；
人，抽到的学生成绩在
记
分，在
记
分，在
记
表示抽取结束后的总记分，求
，
，…， 
后得到如下频率分布直方图．
内的频率；
两型会议桌，每套会议桌需经过加工木材和上油漆两道工序才能完成。已知做一套
的厂房（不管墙高），工程的造价是：