Question

若关于x的方程tx²+（2-3t）x+1=0的两个实根α，β满足0＜α＜1＜β＜2，试求实数t的取值范围．

Answer 1

分析：设出二次不等式相应的二次函数，画出函数的图象，结合图象从判别式、对称轴、区间端点值的符号将根的分布情况列出不等式，求出k的范围．

解答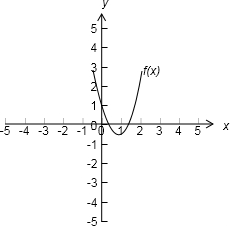：解：设f（x）=tx²+（2-3t）x+1其图象为
∵0＜α＜1＜β＜2
∴

f(1)＜0 f(2)＞0

即

t+2-3t+1＜0 4t+2(2-3t)+1＞0

解得：

3

2

＜t＜

5

2

∴符合题意实数t的取值范围(

3

2

，

5

2

)．

点评：本题考查解决二次不等式实根的分布：结合相应的二次函数的图象，从判别式、对称轴、区间端点值的符号通过不等式限制．